
���� ��1����ʹ�þ��豸����������·��Ҫx�죬��ʹ�����豸��ÿ������·$\frac{1}{x}$��1+40%��������ʵ�ʱ�ԭ�ƻ���ǰ10����������г����̼��ɽ��
��2������������·���ܷ���ΪWԪ����W=12000m+21000n����$\frac{1}{40}$m+$\frac{7}{200}$n=1���õ�m=40-$\frac{7}{5}$n����W=12000����40-$\frac{7}{5}$n��+21000n=480000+4200n������1��n��35������һ�κ����������Լ��ɽ��
��� �⣺��1����ʹ�þ��豸����������·��Ҫx�죬��ʹ�����豸��ÿ������·$\frac{1}{x}$��1+40%�����������
$\frac{15}{x}$+$\frac{1}{x}$��1+40%����x-15-10��=1��
��ã�x=40
��ʹ�þ��豸����������·��Ҫ40�죮
��2������������·���ܷ���ΪWԪ����W=12000m+21000n��
��$\frac{1}{40}$m+$\frac{7}{200}$n=1��
��m=40-$\frac{7}{5}$n��
��W=12000����40-$\frac{7}{5}$n��+21000n=480000+4200n��
��k=4200��0��
��W��n�����������
��1��n��35��$\frac{7}{5}$n��������
�൱n=5ʱ��W����Сֵ����СֵΪ��480000+4200��5=501000��Ԫ����
m=40-$\frac{7}{5}$n=33��
�𣺵�m=5��n=33ʱ����������·���ܷ������٣����ٷ���Ϊ501000Ԫ��
���� ���⿼����һ�κ�����Ӧ�ã���ʽ���̵�ʵ�����ã��ҳ���Ŀ�̺���������ϵ������һ�κ����������Խ����ֵ�����ǽ������Ĺؼ���


 ��������������������ϵ�д�
��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
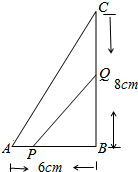 ��ͼ����ABC�У���B=90�㣬��P��A�㿪ʼ��AB���B��1cm/s���ٶ��ƶ�����Q��B�㿪ʼ��BC���C��2cm/s���ٶ��ƶ�����һ��ֹͣ�˶�ʱ��һ��Ҳ��ֹ֮ͣ�˶���
��ͼ����ABC�У���B=90�㣬��P��A�㿪ʼ��AB���B��1cm/s���ٶ��ƶ�����Q��B�㿪ʼ��BC���C��2cm/s���ٶ��ƶ�����һ��ֹͣ�˶�ʱ��һ��Ҳ��ֹ֮ͣ�˶����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
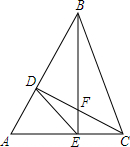 ��ͼ����ABC�У���A=60�㣬��ABC��BE��CD���ڵ�F������˵���У���AD•AB=AE•AC����BF•EF=CF•DF����S��ABC=4S��AED����BC=2DE��������ȷ���У�������
��ͼ����ABC�У���A=60�㣬��ABC��BE��CD���ڵ�F������˵���У���AD•AB=AE•AC����BF•EF=CF•DF����S��ABC=4S��AED����BC=2DE��������ȷ���У�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ij��·����A��B��C��վ��һ������������8ʱ�Ӹ�Aվ5km��P�س�����Cվ������ʻ��15min����Aվ20km
��ͼ��ij��·����A��B��C��վ��һ������������8ʱ�Ӹ�Aվ5km��P�س�����Cվ������ʻ��15min����Aվ20km�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
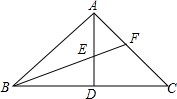 ��ͼ����ABC�У���BAC=90�㣬AD��BC��D��BFƽ�֡�ABC����AD��E������AC��F����֤��$\frac{DE}{AE}=\frac{AF}{CF}$��
��ͼ����ABC�У���BAC=90�㣬AD��BC��D��BFƽ�֡�ABC����AD��E������AC��F����֤��$\frac{DE}{AE}=\frac{AF}{CF}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
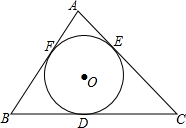 ��ͼ����ABC������Բ��O�����߷ֱ�������D��E��F���㣬AB=7��BC=12��CA=11��
��ͼ����ABC������Բ��O�����߷ֱ�������D��E��F���㣬AB=7��BC=12��CA=11���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com