
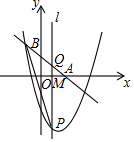
 如图,已知直线y=-$\frac{3}{4}$x+1分别交x轴、y轴于点A、B,M是x轴正半轴上一动点,并以每秒1个单位的速度从O点向x轴正方向运动,过点M作x轴的垂线l,与抛物线y=x2-$\frac{5}{2}$x-2交于点P,与直线AB交于点Q,连结BP,经过t秒时,△PBQ是以BQ为腰的等腰三角形,则t的值是2或$\frac{3+\sqrt{21}}{2}$或$\frac{31}{8}$.
如图,已知直线y=-$\frac{3}{4}$x+1分别交x轴、y轴于点A、B,M是x轴正半轴上一动点,并以每秒1个单位的速度从O点向x轴正方向运动,过点M作x轴的垂线l,与抛物线y=x2-$\frac{5}{2}$x-2交于点P,与直线AB交于点Q,连结BP,经过t秒时,△PBQ是以BQ为腰的等腰三角形,则t的值是2或$\frac{3+\sqrt{21}}{2}$或$\frac{31}{8}$. 分析 分三种情形①当点Q在点P上方时,由BQ=PQ.②当点P在点Q上方时,由BQ=PQ.③当点P在点Q上方时,BQ=BP时.分别列出方程解决问题.
解答 解:∵M(t,0),B(0,1),则Q(t,-$\frac{3}{4}$t+1), P(t,t2-$\frac{5}{2}$t-2),
P(t,t2-$\frac{5}{2}$t-2),
①当点Q在点P上方时,由BQ=PQ得$\frac{5}{4}$t=-$\frac{3}{4}$t+1-t2+$\frac{5}{2}$t+2,解得t=2或-$\frac{3}{2}$(舍弃).
②当点P在点Q下方时,由BQ=PQ得$\frac{5}{4}$t=t2-$\frac{5}{2}$t-2+$\frac{3}{4}$t-1,解得t=$\frac{3+\sqrt{21}}{2}$或$\frac{3-\sqrt{21}}{2}$(舍弃).
③当点P在点Q上方时,BQ=BP时,可得$\frac{-\frac{3}{4}t+1+{t}^{2}-\frac{5}{2}t-2}{2}$=1,解得t=4或-$\frac{3}{4}$(舍弃),
综上所述t为2或$\frac{3+\sqrt{21}}{2}$或4时,△PBQ是以BQ为腰的等腰三角形.
故答案为2或$\frac{3+\sqrt{21}}{2}$或4.
点评 本题考查二次函数、一次函数、等腰三角形的判定和性质等知识,解题的关键是学会分类讨论,学会用方程的思想思考问题,属于中考常考题型.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 200(1+a%)2=108 | B. | 200(1-a2%)=108 | C. | 200(1-2a%)=108 | D. | 200(1-a%)2=108 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 原价 | 每件降价1元 | 每件降价2元 | … | 每件降价x元 | |
| 每件售价(元) | 30 | 29 | 28 | … | 30-x |
| 每天销量(件) | 40 | 42 | 44 | … | 40+2x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
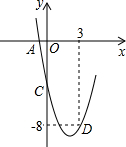 二次函数y=ax2+bx+c的部分图象如图所示,其中图象与x轴交于点A(-1,0),与y轴交于点C(0,-5),且经过点D(3,-8).
二次函数y=ax2+bx+c的部分图象如图所示,其中图象与x轴交于点A(-1,0),与y轴交于点C(0,-5),且经过点D(3,-8).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com