
 已知:如图,点G是CA的延长线上一点,CE交AB于点F,AD∥GE,且∠AGF=∠AFG.求证:AD平分∠BAC.
已知:如图,点G是CA的延长线上一点,CE交AB于点F,AD∥GE,且∠AGF=∠AFG.求证:AD平分∠BAC.  名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
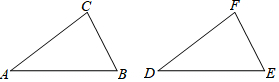
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,AB=4,BC=6,E是BC上一点(不与B、C重合),点P在边CD上运动,M、N分别是AE、PE的中点,线段MN长度的最大值是$\sqrt{13}$.
如图,矩形ABCD中,AB=4,BC=6,E是BC上一点(不与B、C重合),点P在边CD上运动,M、N分别是AE、PE的中点,线段MN长度的最大值是$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
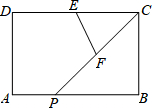 如图,矩形△ABCD中,AB=2,AD=1,E为CD中点,P为AB边上一动点(含端点),F为CP中点,则△CEF的周长最小值为$\sqrt{2}$+1.
如图,矩形△ABCD中,AB=2,AD=1,E为CD中点,P为AB边上一动点(含端点),F为CP中点,则△CEF的周长最小值为$\sqrt{2}$+1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
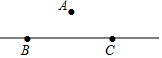 如图,高速公路BC(公路视为直线)的最高限速为120km/h,在该公路正上方离地面20m的点A处设置了一个测速仪,已知在点A测得点B的俯角为45°,点C的俯角为30°,测速仪监测到一辆汽车从点B匀速行驶到点C所用的时间是1.5s,试通过计算,判决该汽车在这段限速路上是否超速.(参考数据:$\sqrt{3}$≈1.7)
如图,高速公路BC(公路视为直线)的最高限速为120km/h,在该公路正上方离地面20m的点A处设置了一个测速仪,已知在点A测得点B的俯角为45°,点C的俯角为30°,测速仪监测到一辆汽车从点B匀速行驶到点C所用的时间是1.5s,试通过计算,判决该汽车在这段限速路上是否超速.(参考数据:$\sqrt{3}$≈1.7)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com