
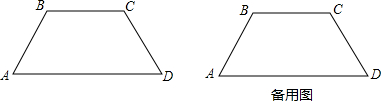
���� ��1�������εĸߣ��õ����κ�����ֱ�������Σ����ݹ��ɶ�����⣻
��2�������ε������ʽ���з�����⣻
��3������Q�ڱ�AB�ϣ���APQ�ǵȱ������Σ���QM=AQ•sin60��=$\frac{\sqrt{3}}{2}$������S��AQP=$\frac{1}{2}$AP•QM=$\frac{1}{2}$•t•$\frac{\sqrt{3}}{2}$t=$\frac{\sqrt{3}}{4}$t2��
����Q�ڰ�BC�ϣ�S��AQP=$\frac{1}{2}$t$•\sqrt{3}$=$\frac{\sqrt{3}}{2}$t��
����Q�ڱ�CD�ϣ���QPD=90�㣬�����PQ������S��AQP=$\frac{1}{2}$AP•PQ=$\frac{1}{2}$•t$•\frac{\sqrt{3}}{2}$��8-2t��=-$\frac{\sqrt{3}}{2}$t2+2$\sqrt{3}$t��
��4����PQΪֱ����Բ������ABCD�ĵ����У�����PQ��AD�����ݣ�1���Ľ��۵ó���3��t��4ʱ����PQΪֱ����Բ������ABCD�ĵ����У�
��� �⣺��1����ͼ1 ����B��BE��AD��E������C��CP��AD��P��
����B��BE��AD��E������C��CP��AD��P��
���ı���BEPC�Ǿ��Σ�
��AB=BC=CD=2��AD=4��
��PE=2��AE=DP=1��
���A=��D=60�㣬
�ߡ�PQDΪֱ�������Σ�
���QPD=90�㼴QP��AD��
��Rt��QPD��
��4-t��2+${��\sqrt{3}��}^{2}$=22��
��t=3��
�൱3��t��4����PQDΪֱ�������Σ�
��2��������ã���ֱ��PQ�����ε�����ȷ֣����Qֻ���ڱ�BC�ϣ���2��t��3����
��S�ı���QPDC=$\frac{1}{2}$S����ABCD��
��$\frac{1}{2}$[��t-2��+t]•$\sqrt{3}$=$\frac{1}{2}��\frac{1}{2}$��2+4��$•\sqrt{3}$��
��t=$\frac{7}{3}$��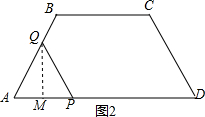
�൱t=$\frac{7}{3}$ʱ��ֱ��PQ�����ε�����ȷ֣�
��3����ͼ2����Q��QM��AD��M��
��0��t��2ʱ����Q�ڱ�AB�ϣ�
QM=AQ•sin60��=$\frac{\sqrt{3}}{2}$��
��S��AQP=$\frac{1}{2}$AP•QM=$\frac{1}{2}$•t•$\frac{\sqrt{3}}{2}$t=$\frac{\sqrt{3}}{4}$t2��
��2��t��3ʱ����Q�ڰ�BC�ϣ�
��S��AQP=$\frac{1}{2}$t$•\sqrt{3}$=$\frac{\sqrt{3}}{2}$t��
��ͼ3��3��t��4ʱ����Q�ڱ�CD�ϣ���QPD=90�㣬
��PQ=DQ•sin60��=$\frac{\sqrt{3}}{2}$��8=2t����
��S��AQP=$\frac{1}{2}$AP•PQ=$\frac{1}{2}$•t$•\frac{\sqrt{3}}{2}$��8-2t��=-$\frac{\sqrt{3}}{2}$t2+2$\sqrt{3}$t��
��4����PQΪֱ����Բ������ABCD�ĵ����У�
��PQ��AD��
�ɣ�1��֪����3��t��4ʱ����QPD=90�㣬
��PQ��AD��
�൱3��t��4ʱ����PQΪֱ����Բ������ABCD�ĵ����У�
���� ������Ҫ�����˵������ε����ʣ����ε�����������ε�����������Ľ���ʽ��Բ��ֱ�ߵ�λ�ù�ϵ��֪ʶ��Ӧ�ã��ر��ǣ�3���У�Ҫ���ݵ�Q�IJ�ͬλ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ABCD�У�EΪBD��һ�㣬��DCE=22.5��
��ͼ��������ABCD�У�EΪBD��һ�㣬��DCE=22.5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com