
 (2012•本溪)如图在直角△ABC中,∠BAC=90°,AB=8,AC=6,DE是AB边的垂直平分线,垂足为D,交边BC于点E,连接AE,则△ACE的周长为( )
(2012•本溪)如图在直角△ABC中,∠BAC=90°,AB=8,AC=6,DE是AB边的垂直平分线,垂足为D,交边BC于点E,连接AE,则△ACE的周长为( )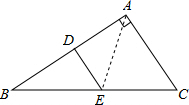 解:连接AE,
解:连接AE,| AB2+AC2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 (2012•本溪)如图,△ABC是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步(小路的宽度不计).观测得点B在点A的南偏东30°方向上,点C在点A的南偏东60°的方向上,点B在点C的北偏西75°方向上,AC间距离为400米.问小金沿三角形绿化区的周边小路跑一圈共跑了多少米?
(2012•本溪)如图,△ABC是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步(小路的宽度不计).观测得点B在点A的南偏东30°方向上,点C在点A的南偏东60°的方向上,点B在点C的北偏西75°方向上,AC间距离为400米.问小金沿三角形绿化区的周边小路跑一圈共跑了多少米?| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•本溪)如图,矩形ABCD中,点P、Q分别是边AD和BC的中点,沿过C点的直线折叠矩形ABCD使点B落在线段PQ上的点F处,折痕交AB边于点E,交线段PQ于点G,若BC长为3,则线段FG的长为
(2012•本溪)如图,矩形ABCD中,点P、Q分别是边AD和BC的中点,沿过C点的直线折叠矩形ABCD使点B落在线段PQ上的点F处,折痕交AB边于点E,交线段PQ于点G,若BC长为3,则线段FG的长为| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| S |
| 4n-1 |
| S |
| 4n-1 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com