【题目】如图，在每个小正方形的边长为
的网格中，点A，B，C在格点上，以点A为圆心、AC为半径的半圆交AB于点 E．
（1）BE的长为________；
（2）请用无刻度的直尺，在如图所示的网格中，找一点P（点P，C 在AB两侧），使PA=5，PE与半圆相切. 简要说明点P的位置是如何找到的．
【答案】（1）2；（2）图见解析，理由见解析．
【解析】
（1）先结合网格的特点可得
，再根据勾股定理可得
，然后根据圆的性质可得
，最后根据线段的和差即可得；
（2）取格点
，分别作直线
，两直线相交于点P，点P即为所作；理由：先根据平行四边形的判定与性质得出
，再根据三角形全等的判定定理与性质得出
，然后根据三角形中位线定理、垂直平分线的判定与性质可得
，由此即可得证．
（1）由网格的特点得：
由圆的性质得：
故答案为：2；
（2）如图，取格点，分别作直线，两直线相交于点P，则点P即为所作，理由如下：
由网格的特点得：
，
，
四边形ABGF是平行四边形
在
和
中，
，即
与半圆相切
，即点A是DF的中点，且
是
的中位线，点E是DP的中点
垂直平分DP
综上，点P即为所作．
科目：初中数学 来源： 题型：
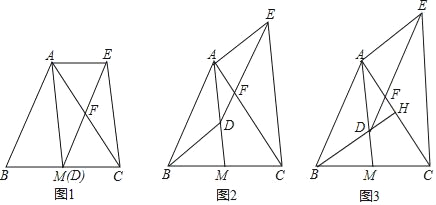
【题目】如图，AM是△ABC的中线，D是线段AM上一点（不与点A重合）．DE∥AB交AC于点F，CE∥AM，连结AE．
（1）如图1，当点D与M重合时，求证：四边形ABDE是平行四边形；
（2）如图2，当点D不与M重合时，（1）中的结论还成立吗？请说明理由．
（3）如图3，延长BD交AC于点H，若BH⊥AC，且BH=AM．
①求∠CAM的度数；
②当FH=
，DM=4时，求DH的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
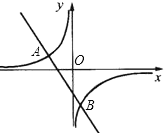
【题目】如图，一次函数y＝kx+b的图象与反比例函数y＝
的图象交于A（﹣2，1），B（1，n）两点．
（1）求反比例函数和一次函数的解析式；
（2）根据图象写出使一次函数的值＞反比例函数的值的x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线
（
，
，
是常数，
）经过点A（
，
）和点B （，
），且抛物线的对称轴在
轴的左侧. 下列结论： ① 
； ② 方程
有两个不等的实数根； ③
. 其中，正确结论的个数是（ ）.
A.0B.1C.2D.3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两个种子店都销售“黄金1号”玉米种子．在甲店，该种子的价格为 5元 / kg，如果一次购买2 kg 以上的种子，超过 2 kg 部分的种子的价格打8折．在乙店，不论一次购买该种子的数量是多少，价格均为4.5 元 / kg．
（1）根据题意，填写下表：
（2）设一次购买种子的数量为
kg（
）. 在甲店购买的付款金额记为
元，在乙店购买的付款金额为
元，分别求，关于的函数解析式；
（3） 若在同一店中一次购买种子的付款金额是36元，则最多可购买种子______ kg.若在同一店中一次购买种子10 kg，则最少付款金额是________元.
查看答案和解析>>
科目：初中数学 来源： 题型：
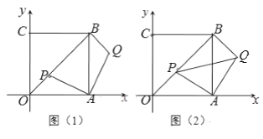
【题目】平面直角坐标系中，四边形OABC是正方形，点A，C 在坐标轴上，点B（
，），P是射线OB上一点，将
绕点A顺时针旋转90°，得
，Q是点P旋转后的对应点.
（1）如图（1）当OP = 
时，求点Q的坐标；
（2）如图（2），设点P（
，
）（
），
的面积为S. 求S与的函数关系式，并写出当S取最小值时，点P的坐标；
（3）当BP+BQ = 
时，求点Q的坐标（直接写出结果即可）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线
：
与
轴、
轴交于
、
两点，与反比例函数
的图像交于点
，且
．
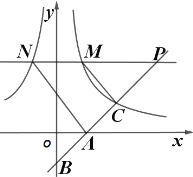
（1）求反比例函数的解析式；
（2）点
是直线上一点，过点
作轴的平行线交反比例函数和
的图像于
，
两点，连
，
，当
时，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
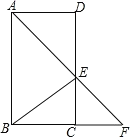
【题目】如图，在ABCD中，∠BAD的平分线交CD于点E，交BC的延长线于 点F，连接BE，∠F=45°．
（1）求证：四边形ABCD是矩形；(2)若AB=14，DE=8，求sin∠AEB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
