
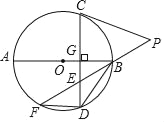
【题目】如图,AB为⊙O的直径,CD⊥AB于点G,E是CD上一点,且BE=DE,延长EB至点P,连结CP,使PC=PE,延长BE与⊙O交于点F,连结BD,FD.
(1)求证:CD=BF;
(2)求证:PC是⊙O的切线;
(3)若tanF=![]() ,AG﹣BG=
,AG﹣BG=![]() ,求ED的值.
,求ED的值.
【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】
(1)连接![]() ,由于
,由于![]() ,
,![]() ,
,![]() ,从而得证;
,从而得证;
(2)连接![]() ,由于
,由于![]() ,
,![]() ,从而可得
,从而可得![]() ,又因为
,又因为![]() ,从而可知
,从而可知![]() ,由于
,由于![]() ,
,![]() ,所以
,所以![]() ,从而得证;
,从而得证;
(3)连接![]() ,易证
,易证![]() ,所以
,所以![]() ,即
,即![]() ,从而可求出
,从而可求出![]() 的长度,再由勾股定理可知
的长度,再由勾股定理可知![]() 的长度,由于
的长度,由于![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,从而可求出
,从而可求出![]() 的值.
的值.
(1)连接BC,
∵BE=DE,
∴∠BDE=∠DBE,
在△BCD与△DFB中,
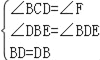
∴△BCD≌△DFB(AAS)
∴CD=BF
(2)连接OC,
∵∠COB=2∠CDB,∠CEB=∠CDB+∠DBE=2∠CDB
∴∠COB=∠CEB,
∵PC=PE,
∴∠COB=∠CEB=∠PCE,
∵AB⊥CD,
∴∠COB+∠OCG=90°,
∴∠PCE+∠OCG=∠PCO=90°,
∴OC⊥CP
∵OC是半径,
∴PC是⊙O的切线,
(3)连接AD,
∵AB是直径,
∴∠ADB=90°,
∵AB⊥CD,
∴![]() =
=![]() ,
,
∴∠BDG=∠A=∠F
∵tan∠F=![]()
∴tan∠A=![]() =
=![]() ,即AG=
,即AG=![]() GD
GD
同理可得:BG=![]() GD,
GD,
∴AG﹣BG=![]() GD﹣
GD﹣![]() GD=
GD=![]()
![]() ,
,
解得:GD=2![]() ,
,
∴CD=2GD=4![]() ,
,
∴BG=![]()
![]()
∴由勾股定理可知:BD=![]()
![]()
∵∠BCD=∠EDB,∠BDC=∠EBD,
∴△BCD∽△EDB
∴![]() =
=![]()
∵BC=BD,
∴ED=![]() =
=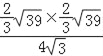 =
=![]()


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB、BC、AC三边的长分别为![]() ,
, ![]() ,
, ![]() ,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)△ABC的面积为 .
(2)若△DEF的三边DE、EF、DF长分别为![]() ,
, ![]() ,
, ![]() ,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
(3)在△ABC中,AB=2![]() ,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠ECF=∠BCD=90°,CE=CF=5,BC=7,BD平分∠ABC,E是△BCD内一点,F是四边形ABCD外一点.(E可以在△BCD的边上)
(1)求证:DC=BC;
(2)当∠BEC=135°,设BE=a,DE=b,求a与b满足的关系式;
(3)当E落在线段BD上时,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
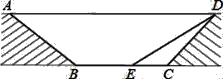
【题目】为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行,通道水平宽度BC为8米,∠BCD=135°,通道斜面CD的长为6米,通道斜面AB的坡度i=1:![]() .
.
(1)求通道斜面AB的长;
(2)为增加市民行走的舒适度,拟将设计图中的通道斜面CD的坡度变缓,修改后的通道斜面DE的坡角为30°,求此时BE的长.
(答案均精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈2.24,
≈2.24,![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′,B′,C′三点的坐标:A′( ),B′( ),C′( )
(3)计算△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=120,AD⊥BC,且AD=AB.
(1)如图1,DE⊥AB,DF⊥AC,垂足分别为点E,F,求证:AE+AF=AD
(2)如图2,如果∠EDF=60,且∠EDF两边分别交边AB,AC于点E,F,那么线段AE,AF,AD之间有怎样的数量关系?并给出证明.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,下列判断正确的是( )
A. 1一定不是关于x的方程x2+bx+a=0的根
B. 0一定不是关于x的方程x2+bx+a=0的根
C. 1和﹣1都是关于x的方程x2+bx+a=0的根
D. 1和﹣1不都是关于x的方程x2+bx+a=0的根
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com