
 如图,点C在线段AB上(不与端点重合),点D、E在AB同侧,且AD∥CE,CD∥BE,连接AE交CD于M,连接BD交CE于N.
如图,点C在线段AB上(不与端点重合),点D、E在AB同侧,且AD∥CE,CD∥BE,连接AE交CD于M,连接BD交CE于N.分析 (1)根据△ACD和△BCE是等腰直角三角形,得到∠DAC=∠ECB=45°,推出CE∥AD,即可得到结论,由△AMD∽△EMC,得到$\frac{AM}{NE}$=$\frac{AD}{CE}$,由△CND∽△ENB;得到$\frac{CN}{NE}=\frac{DC}{BE}$,等量代换得到$\frac{CN}{NE}=\frac{AM}{ME}$,即可得到结论;
(2)根据相似三角形的判定定理得到△CND∽△ENB,由相似三角形的性质得到$\frac{CN}{NE}$=$\frac{DN}{NB}$,设$\frac{CN}{NE}$=$\frac{DN}{NB}$=k,则CN=kNE,DN=kNB,根据平行线分线段成比例得到$\frac{MN}{AC}$=$\frac{NE}{CE}$=$\frac{NE}{NE+CN}$=$\frac{1}{k+1}$,$\frac{MN}{BC}$=$\frac{DN}{DB}$=$\frac{1}{k+1}$,结论得到结论.
解答 解:(1)∵△ACD和△BCE是等腰直角三角形,
∴∠DAC=∠ECB=45°,
∴CE∥AD,
∴△AMD∽△EMC,
∴$\frac{AM}{NM}$=$\frac{AD}{CE}$,
∵△ACD和△BCE是等腰直角三角形,
∴∠ACD=∠CBE=45°,
∴CD∥BE,
∴△CND∽△ENB;
∴$\frac{CN}{NE}$=$\frac{DC}{BE}$
∴CD=AD,BE=CE,
∴$\frac{CN}{NE}=\frac{AM}{ME}$,
∴MN∥AB;
(2)∵CD∥BE,
∴△CND∽△ENB,
∴$\frac{CN}{NE}$=$\frac{DN}{NB}$,
设$\frac{CN}{NE}$=$\frac{DN}{NB}$=k,
则CN=kNE,DN=kNB,
∵MN∥AB,
∴$\frac{MN}{AC}$=$\frac{NE}{CE}$=$\frac{NE}{NE+CN}$=$\frac{1}{k+1}$,$\frac{MN}{BC}$=$\frac{DN}{DB}$=$\frac{1}{k+1}$,
∴$\frac{MN}{AC}$+$\frac{MN}{BC}$=1,
∴$\frac{1}{MN}$=$\frac{1}{AC}$+$\frac{1}{BC}$.
点评 本题考查了相似三角形的判定和性质,等腰三角形的性质,熟练掌握相似三角形的判定和性质是解题的关键.


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
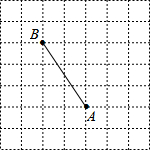 在7×7的方格中,每个小方格的边长均为1,A、B两点都在格点上,若在格点上找到一点P,使△PAB的面积为6,则符合条件的点P有( )
在7×7的方格中,每个小方格的边长均为1,A、B两点都在格点上,若在格点上找到一点P,使△PAB的面积为6,则符合条件的点P有( )| A. | 2个 | B. | 4个 | C. | 8个 | D. | 12个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在梯形ABCD中,AD∥BC,点E、F分别在边AB、CD上.EF∥BC,EF交AC于G.EB=DF,AE=9,CF=4.求BE,CD,$\frac{GF}{AD}$的值.
在梯形ABCD中,AD∥BC,点E、F分别在边AB、CD上.EF∥BC,EF交AC于G.EB=DF,AE=9,CF=4.求BE,CD,$\frac{GF}{AD}$的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AD平分∠BAC,过D作DE∥AC交AB于E,过E作AD的垂线交AD于O,交BC的延长线于F,连接AF,求证:∠CAF=∠B.
如图,在△ABC中,AD平分∠BAC,过D作DE∥AC交AB于E,过E作AD的垂线交AD于O,交BC的延长线于F,连接AF,求证:∠CAF=∠B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 598 | B. | 602 | C. | 604 | D. | 608 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 菏泽牡丹博览会国花馆展厅志愿者的年龄分布如图,这些志愿者年龄的中位数和众数分别是( )
菏泽牡丹博览会国花馆展厅志愿者的年龄分布如图,这些志愿者年龄的中位数和众数分别是( )| A. | 20岁,19岁 | B. | 20岁,20岁 | C. | 21岁,20岁 | D. | 22岁,20岁 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com