练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若直线与直线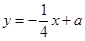相交于x轴上，则直线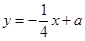不经过（　　）

    A、第一象限　　　　B、第二象限　　　C、第三象限　　　　D、第四象限

     

    【答案】

    C

    【解析】本题考查了一次函数与二元一次方程组. 根据直线与直线相交于x轴上，则可求出a的值，然后即可得出答案．

    解：直线与直线相交于x轴上，

    ∴

    解得：

    ∵两直线相交于x轴上，故=0，

    解得：a=1，∴y=，

    故y=x+a不经过第三象限，

    故选C．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图6，在平面直角坐标系中，直线分别交轴、轴于点将绕点顺时针旋转90后得到.

    （1）求直线的解析式；
    （2）若直线与直线相交于点，求的面积.

    查看答案和解析>>

    科目：初中数学 来源：第5章《反比例函数》中考题集（24）：3、反比例函数的应用（解析版） 题型：解答题

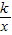    已知双曲线y=与直线y=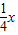相交于A、B两点．第一象限上的点M（m，n）（在A点左侧）是双曲线y=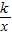上的动点．过点B作BD∥y轴交x轴于点D．过N（0，-n）作NC∥x轴交双曲线y=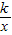于点E，交BD于点C．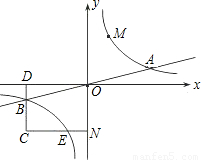
    （1）若点D坐标是（-8，0），求A、B两点坐标及k的值；
    （2）若B是CD的中点，四边形OBCE的面积为4，求直线CM的解析式；
    （3）设直线AM、BM分别与y轴相交于P、Q两点，且MA=pMP，MB=qMQ，求p-q的值．

    查看答案和解析>>

    科目：初中数学 来源：第20章《二次函数和反比例函数》常考题集（43）：20.7 反比例函数的图象、性质和应用（解析版） 题型：解答题

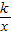    已知双曲线y=与直线y=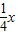相交于A、B两点．第一象限上的点M（m，n）（在A点左侧）是双曲线y=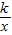上的动点．过点B作BD∥y轴交x轴于点D．过N（0，-n）作NC∥x轴交双曲线y=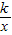于点E，交BD于点C．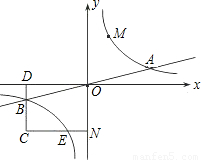
    （1）若点D坐标是（-8，0），求A、B两点坐标及k的值；
    （2）若B是CD的中点，四边形OBCE的面积为4，求直线CM的解析式；
    （3）设直线AM、BM分别与y轴相交于P、Q两点，且MA=pMP，MB=qMQ，求p-q的值．

    查看答案和解析>>

    科目：初中数学 来源：2012年广东省广州市聚贤暨四中中考数学一模试卷（解析版） 题型：解答题

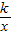    已知双曲线y=与直线y=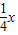相交于A、B两点．第一象限上的点M（m，n）（在A点左侧）是双曲线y=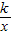上的动点．过点B作BD∥y轴交x轴于点D．过N（0，-n）作NC∥x轴交双曲线y=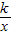于点E，交BD于点C．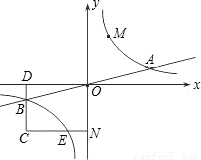
    （1）若点D坐标是（-8，0），求A、B两点坐标及k的值；
    （2）若B是CD的中点，四边形OBCE的面积为4，求直线CM的解析式；
    （3）设直线AM、BM分别与y轴相交于P、Q两点，且MA=pMP，MB=qMQ，求p-q的值．

    查看答案和解析>>

    科目：初中数学 来源：2009年江苏省连云港市中考数学原创试卷大赛（16）（解析版） 题型：解答题

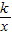    （2008•南通）已知双曲线y=与直线y=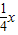相交于A、B两点．第一象限上的点M（m，n）（在A点左侧）是双曲线y=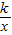上的动点．过点B作BD∥y轴交x轴于点D．过N（0，-n）作NC∥x轴交双曲线y=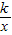于点E，交BD于点C．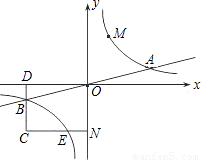
    （1）若点D坐标是（-8，0），求A、B两点坐标及k的值；
    （2）若B是CD的中点，四边形OBCE的面积为4，求直线CM的解析式；
    （3）设直线AM、BM分别与y轴相交于P、Q两点，且MA=pMP，MB=qMQ，求p-q的值．

    查看答案和解析>>

    同步练习册答案