
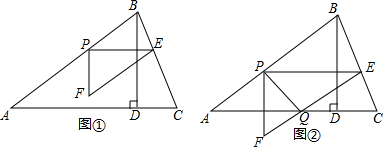
·ÖĪö £Ø1£©·Ö±šĒó³öADŗĶCDµÄ³¤£¬Ļą¼Ó¼“æÉ£»
£Ø2£©µ±EF¾¹żµćDŹ±£¬ČēĶ¼2£¬øł¾ŻDE=AP=DCĮŠŹ½µĆ£ŗt=1£»µ±FŌŚAC±ßÉĻŹ±£¬ČēĶ¼4£¬ÓÉEF=CFµĆ£ŗt=5-$\frac{4}{5}$t£¬t=$\frac{25}{9}$£»ŌŁ·ÖĮ½ÖÖĒéæö·Ö±š¼ĘĖćÖŲµžĖıߊĪµÄĆ껿¼“æÉ£»
£Ø3£©¢Łµ±PQ½«”÷PEFµÄĆ껿·Ö³É1£ŗ2Į½²æ·ÖŹ±£¬ŅŖ·ÖĮ½ÖÖĒéæö£ŗµ±S”÷PQF£ŗS”÷PQE=1£ŗ2ŗĶµ±S”÷PQF£ŗS”÷PQE=2£ŗ1Ź±£¬·Ö±š“śČė$\frac{{S}_{”÷PQE}}{{S}_{”÷PEF}}$ÖŠĮŠµČŹ½æÉĒóµĆtµÄÖµ£»
¢Ś·ÖĮ½ÖÖĒéæö£ŗ
i£©µ±PQµÄÖŠ“¹Ļß¹żµćAŹ±£¬ČēĶ¼7£¬øł¾ŻPE=PAĮŠµČŹ½µĆ½įĀŪ£¬
ii£©µ±PQµÄÖŠ“¹Ļß¹żBŹ±£¬ČēĶ¼8£¬ŌņPB=BQ=5-t£¬ŌŚRt”÷BQDÖŠ£¬ĮŠ·½³Ģ42+£Øt-2£©2=£Ø5-t£©2£¬½ā³ö¼“æÉ£®
½ā“š 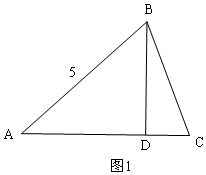 ½ā£ŗ£Ø1£©ŌŚRt”÷BDCÖŠ£¬tan”ĻC=$\frac{BD}{CD}$=3£¬
½ā£ŗ£Ø1£©ŌŚRt”÷BDCÖŠ£¬tan”ĻC=$\frac{BD}{CD}$=3£¬
”ßBD=3£¬
”ąCD=1£¬
ŌŚRt”÷ABDÖŠ£¬Óɹ“¹É¶ØĄķµĆ£ŗAD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4£¬
”ąAC=AD+CD=4+1=5£»
£Ø2£©ÓÉĢāŅāµĆ£ŗAP=t£¬
µ±EF¾¹żµćDŹ±£¬ČēĶ¼2£¬
”ßPE”ĪAC£¬EF”ĪAP£¬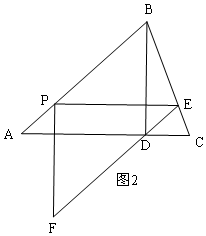
”ąĖıߊĪPADEŹĒĘ½ŠŠĖıߊĪ£¬
”ąDE=AP=t£¬
”ßAB=AC=5£¬
”ą”ĻC=”ĻABC£¬
”ßEF”ĪAB£¬
”ą”ĻABC=”ĻDEC£¬
”ą”ĻDEC=”ĻC£¬
”ąDE=DC£¬
”ąt=1£»
¢Łµ±0”Üt”Ü1Ź±£¬ČēĶ¼3£¬”÷PEFÓė”÷ABDÖŲµž²æ·ÖĶ¼ŠĪµÄĆ껿ĪŖĖıߊĪPGDHµÄĆ껿£¬
”ß”ĻEPF=90”ć£¬PE”ĪAC£¬
”ą”ĻPGC=90”ć£¬
”ßBD”ĶAC£¬
”ą”ĻADB=90”ć£¬
”ą”ĻADB=”ĻPGC=”ĻEPF=90”ć£¬
”ąĖıߊĪPGDHŹĒ¾ŲŠĪ£¬
ŌŚRt”÷APGÖŠ£¬sin”ĻA=$\frac{BD}{AB}=\frac{PG}{AP}$£¬
”ą$\frac{3}{5}=\frac{PG}{t}$£¬
”ąPG=$\frac{3t}{5}$£¬
”ąAG=$\frac{4t}{5}$£¬
”ąGD=AD-AG=4-$\frac{4t}{5}$£¬
”ąS=S¾ŲŠĪPGDH=PG•GD=$\frac{3t}{5}$£Ø4-$\frac{4t}{5}$£©=-$\frac{12}{25}{t}^{2}$+$\frac{12}{5}t$£»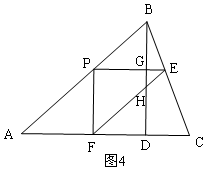
¢Śµ±FŌŚAC±ßÉĻŹ±£¬ČēĶ¼4£¬
AF=$\frac{4}{5}$t£¬CF=5-$\frac{4}{5}$t
ÓÉEF=CFµĆ£ŗt=5-$\frac{4}{5}$t
t=$\frac{25}{9}$£»
µ±$\frac{25}{9}$”Üt”Ü5Ź±£¬ČēĶ¼5£¬”÷PEFÓė”÷ABDÖŲµž²æ·ÖĶ¼ŠĪµÄĆ껿ĪŖĖıߊĪPFHGµÄĆ껿£¬
”ßPE”ĪAC£¬
”ą”÷BPE”×”÷BAD£¬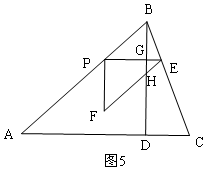
”ą$\frac{PB}{AB}=\frac{PG}{AD}$£¬
”ą$\frac{PG}{4}=\frac{5-t}{5}$£¬
”ąPG=$\frac{4}{5}£Ø5-t£©$£¬
”ßPE=PB=5-t£¬
”ąGE=5-t-$\frac{4}{5}$£Ø5-t£©=$\frac{1}{5}$£Ø5-t£©£¬
”ßEF”ĪAB£¬
”ą”ĻEHG=”ĻABD£¬
”ątan”ĻABD=tan”ĻEHG=$\frac{AD}{BD}=\frac{GE}{GH}$£¬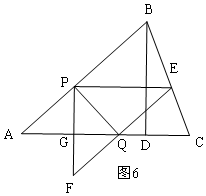
”ą$\frac{4}{3}=\frac{\frac{1}{5}£Ø5-t£©}{GH}$£¬
”ąGH=$\frac{3}{20}$£Ø5-t£©£¬
Ķ¬ĄķµĆ£ŗ$\frac{4}{3}=\frac{5-t}{PF}$£¬
PF=$\frac{3£Ø5-t£©}{4}$£¬
”ąS=SĢŻŠĪPFHG=$\frac{1}{2}$£ØGH+PF£©•PG=$\frac{1}{2}$[$\frac{3}{20}$£Ø5-t£©+$\frac{3}{4}$£Ø5-t£©]$•\frac{4}{5}$£Ø5-t£©=$\frac{9}{25}$£Ø5-t£©2=$\frac{9}{25}{t}^{2}-\frac{18}{5}t+9$£»
£Ø3£©¢ŁPE=BP=5-t£¬PF=$\frac{3}{4}£Ø5-t£©$£¬PG=$\frac{3t}{5}$£¬
µ±S”÷PQF£ŗS”÷PQE=1£ŗ2Ź±£¬$\frac{{S}_{”÷PQE}}{{S}_{”÷PEF}}$=$\frac{2}{3}$£¬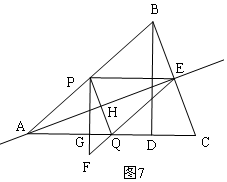
¼“$\frac{\frac{1}{2}£Ø5-t£©•\frac{3}{5}t}{\frac{1}{2}£Ø5-t£©•\frac{3}{4}£Ø5-t£©}$=$\frac{2}{3}$£¬½āµĆ£ŗt=$\frac{25}{11}$£¬AP=$\frac{25}{11}$£¬
µ±S”÷PQF£ŗS”÷PQE=2£ŗ1Ź±£¬$\frac{{S}_{”÷PQE}}{{S}_{”÷PEF}}$=$\frac{1}{3}$£¬
¼“$\frac{\frac{1}{2}£Ø5-t£©•\frac{3}{5}t}{\frac{1}{2}£Ø5-t£©•\frac{3}{4}£Ø5-t£©}$=$\frac{1}{3}$£¬½āµĆ£ŗt=$\frac{25}{17}$£¬AP=$\frac{25}{17}$£¬
ŌņAPµÄ³¤ŹĒ$\frac{25}{11}$»ņ$\frac{25}{17}$£»
¢Ś·ÖĮ½ÖÖĒéæö£ŗ
i£©µ±PQµÄÖŠ“¹Ļß¹żµćAŹ±£¬ČēĶ¼7£¬¼“AEŹĒPQµÄÖŠ“¹Ļߣ¬
”ßĖıߊĪPAQEŹĒĘ½ŠŠĖıߊĪ£¬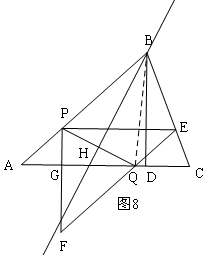
AE”ĶPQ£¬
”ą?PAQEŹĒĮāŠĪ£¬
”ąPE=PA£¬
”ąt=5-t£¬
t=$\frac{5}{2}$£¬
ii£©µ±PQµÄÖŠ“¹Ļß¹żBŹ±£¬ČēĶ¼8£¬Į¬½ÓEQ£¬ŌņPB=BQ=5-t£¬
”ßCQ=EQ=t£¬
”ąQD=CQ-CD=t-2£¬
ŌŚRt”÷BQDÖŠ£¬42+£Øt-2£©2=£Ø5-t£©2£¬
½āµĆ£ŗt=$\frac{5}{6}$£¬
×ŪÉĻĖłŹö£¬PQµÄ“¹Ö±Ę½·ÖĻß¾¹ż”÷ABCµÄ¶„µćŹ±tµÄÖµŹĒ$\frac{5}{2}$»ņ$\frac{5}{6}$£®
µćĘĄ ±¾ĢāŹĒČż½ĒŠĪµÄ×ŪŗĻĢā£¬æ¼²éĮĖ¶ÆµćŌĖ¶ÆĪŹĢā”¢¹“¹É¶ØĄķ”¢Ę½ŠŠĖıߊĪŗĶĮāŠĪµÄŠŌÖŹŗĶÅŠ¶Ø”¢Čż½ĒŗÆŹż¼°ø÷ĄąĶ¼ŠĪĆ껿µÄĒó·Ø£¬±Č½Ļø“ŌÓ£¬ÓČĘäŹĒµŚ¶žĪŹ£¬¼ĘĖćÖŲµž²æ·ÖĶ¼ŠĪĆ껿Ź±£¬Ņ»ŅŖĻČĒóĢŲŹāĪ»ÖĆŹ±tµÄÖµ£¬¶žŅŖĄūÓĆŹżŠĪ½įŗĻµÄĖ¼Ļė£¬ĻČ¹Ū²ģĶ¼ŠĪµÄĢŲµć£¬ŌŁČ·¶ØĆ껿µÄĒó·Ø£®


 æĪæĪÓÅÄÜĮ¦ÅąÓÅ100·ÖĻµĮŠ“š°ø
æĪæĪÓÅÄÜĮ¦ÅąÓÅ100·ÖĻµĮŠ“š°ø ÓÅ°Ł·ÖæĪŹ±»„¶ÆĻµĮŠ“š°ø
ÓÅ°Ł·ÖæĪŹ±»„¶ÆĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 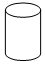 | B£® | 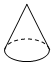 | C£® | 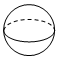 | D£® | 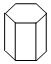 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
 ČēĶ¼£¬ŅŃÖŖPŹĒĻ߶ĪABµÄÖŠµć£¬µćC”¢D°ŃĻ߶ĪABČżµČ·Ö£¬ČōCP=2£¬ŌņABµÄ³¤ĪŖ12£®
ČēĶ¼£¬ŅŃÖŖPŹĒĻ߶ĪABµÄÖŠµć£¬µćC”¢D°ŃĻ߶ĪABČżµČ·Ö£¬ČōCP=2£¬ŌņABµÄ³¤ĪŖ12£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ¾ŲŠĪABCDÖŠ£¬µćE”¢F·Ö±šŌŚ±ßCD”¢ABÉĻ£¬ĒŅDE=BF£®”ĻECA=”ĻFCA£®
¾ŲŠĪABCDÖŠ£¬µćE”¢F·Ö±šŌŚ±ßCD”¢ABÉĻ£¬ĒŅDE=BF£®”ĻECA=”ĻFCA£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
 ČēĶ¼ŌŚ×ų±źĻµÖŠ·ÅÖĆŅ»ĮāŠĪOABC£¬ŅŃÖŖ”ĻABC=60”ć£¬OA=1£®ĻČ½«ĮāŠĪOABCŃŲxÖįµÄÕż·½ĻņĪŽ»¬¶Æ·×Ŗ£¬Ćæ“Ī·×Ŗ60”ć£¬Į¬Šų·×Ŗ2015“Ī£¬µćAµÄĀäµćŅĄ“ĪĪŖA1£¬A2£¬A3£¬”£¬ŌņA2015µÄ×ų±źĪŖ£®£Ø””””£©
ČēĶ¼ŌŚ×ų±źĻµÖŠ·ÅÖĆŅ»ĮāŠĪOABC£¬ŅŃÖŖ”ĻABC=60”ć£¬OA=1£®ĻČ½«ĮāŠĪOABCŃŲxÖįµÄÕż·½ĻņĪŽ»¬¶Æ·×Ŗ£¬Ćæ“Ī·×Ŗ60”ć£¬Į¬Šų·×Ŗ2015“Ī£¬µćAµÄĀäµćŅĄ“ĪĪŖA1£¬A2£¬A3£¬”£¬ŌņA2015µÄ×ų±źĪŖ£®£Ø””””£©| A£® | £Ø1343£¬0£© | B£® | £Ø1347£¬0£© | C£® | £Ø1343$\frac{1}{2}$£¬$\frac{\sqrt{3}}{2}$£© | D£® | £Ø1347$\frac{1}{2}$£¬$\frac{\sqrt{3}}{2}$£© |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com