
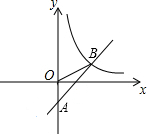
 如图,在平面直角坐标系中,直线AB与y轴相交于点A(0,-2),与反比例函数在第一象限内的图象相交于点B(m,2),△AOB的面积为4.
如图,在平面直角坐标系中,直线AB与y轴相交于点A(0,-2),与反比例函数在第一象限内的图象相交于点B(m,2),△AOB的面积为4.分析 (1)根据△AOB的面积为4,A(0,-2),即可得到B点坐标为(4,2),进而得出k=4×2=8,设直线AB函数关系式为y=nx-2,把(4,2)代入,得n的值;
(2)过点O作OD⊥AB于点D,设AB与x轴相交于点E,由直线AB:y=x-2可得,OA=OE=2,∠OAE=45°,由B点坐标为(4,2),可得OB=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,据此可得sin∠OBA的值.
解答 解:(1)∵△AOB的面积为4,A(0,-2),
∴$\frac{1}{2}$OA×xB=$\frac{1}{2}$×2×xB=4,
∴xB=4,
∴B点坐标为(4,2),
设反比例函数关系式为y=$\frac{k}{x}$,
∴k=4×2=8,
反比例函数关系式为y=$\frac{8}{x}$,
设直线AB函数关系式为y=nx-2,
把(4,2)代入,得4n-2=2,
∴n=1,
∴直线AB函数关系式为y=x-2;
(2)如图,过点O作OD⊥AB于点D,设AB与x轴相交于点E,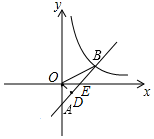
由直线AB:y=x-2可得,OA=OE=2,
∴∠OAE=45°
∴OD=OA•sin45°=$\sqrt{2}$,
由B点坐标为(4,2),可得OB=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
∴sin∠OBA=$\frac{OD}{OB}$=$\frac{\sqrt{2}}{2\sqrt{5}}$=$\frac{\sqrt{10}}{10}$.
点评 本题主要考查了反比例函数与一次函数交点问题,解题时注意:反比例函数与一次函数交点坐标同时满足反比例函数与一次函数解析式.解决问题的关键是作辅助线构造直角三角形.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:解答题
 某初中校对学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:
某初中校对学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:| 各年级学生成绩统计表 | ||||
| 优秀 | 良好 | 合格 | 不合格 | |
| 七年级 | 28 | 20 | a | 8 |
| 八年级 | 29 | 13 | 13 | 5 |
| 九年级 | 24 | 15 | 14 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 开口向上,对称轴是y轴,顶点是原点 | |
| B. | 开口向下,对称轴是y轴,顶点是原点 | |
| C. | 对称轴是y轴,顶点是原点 | |
| D. | 函数y的最小值为0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
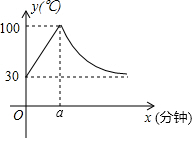 教室内的饮水机接通电源进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(分钟)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.如图为在水温为30℃时,接通电源后,水温y(℃)和时间x(分钟)的关系如图.
教室内的饮水机接通电源进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(分钟)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.如图为在水温为30℃时,接通电源后,水温y(℃)和时间x(分钟)的关系如图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (1,-3) | C. | (3,-1) | D. | (3,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com