
 甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:分析 (1)根据速度=高度÷时间即可算出甲登山上升的速度;根据高度=速度×时间即可算出乙在A地时距地面的高度b的值;
(2)分0≤x≤2和x≥2两种情况,根据高度=初始高度+速度×时间即可得出y关于x的函数关系;
(3)找出甲登山全程中y关于x的函数关系式,令二者做差等于50即可得出关于x的一元一次方程,解之即可得出结论.
解答 解:(1)(300-100)÷20=10(米/分钟),
b=15÷1×2=30.
故答案为:10;30.
(2)当0≤x≤2时,y=15x;
当x≥2时,y=30+10×3(x-2)=30x-30.
当y=30x-30=300时,x=11.
∴乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=$\left\{\begin{array}{l}{15x(0≤x≤2)}\\{30x-30(2≤x≤11)}\end{array}\right.$.
(3)甲登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=10x+100(0≤x≤20).
当10x+100-(30x-30)=50时,解得:x=4;
当30x-30-(10x+100)=50时,解得:x=9;
当300-(10x+100)=50时,解得:x=15.
答:登山4分钟、9分钟或15分钟时,甲、乙两人距地面的高度差为50米.
点评 本题考查了一次函数的应用以及解一元一次方程,解题的关键是:(1)根据数量关系列式计算;(2)根据高度=初始高度+速度×时间找出y关于x的函数关系式;(3)将两函数关系式做差找出关于x的一元一次方程.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
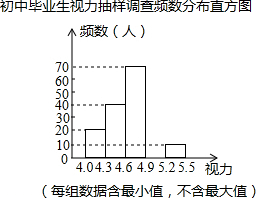 某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图,请根据图表信息回答下列问题:
某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图,请根据图表信息回答下列问题:| 视力 | 频数(人) | 频率 |
| 4.0≤x<4.3 | 20 | 0.1 |
| 4.3≤x<4.6 | 40 | 0.2 |
| 4.6≤x<4.9 | 70 | 0.35 |
| 4.9≤x<5.2 | a | 0.3 |
| 5.2≤x<5.5 | 10 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
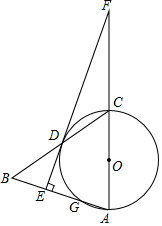 如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC的中点,DE⊥AB,垂足为E,交AC的延长线于点F.
如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC的中点,DE⊥AB,垂足为E,交AC的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com