
 如图,在直角坐标系中,每条横线和竖线代表一条路,小明从学校(点O)放学回家(点P),沿途依次经过超市C,书店B,邮局A.请你画出最短的路径,用点的坐标表示依次经过的十字路口,请问最短路径有几条?
如图,在直角坐标系中,每条横线和竖线代表一条路,小明从学校(点O)放学回家(点P),沿途依次经过超市C,书店B,邮局A.请你画出最短的路径,用点的坐标表示依次经过的十字路口,请问最短路径有几条? 分析 分别找到从O到C、从C到B、从B到A、从A到P的最短路径即可得.
解答 解:如图所示,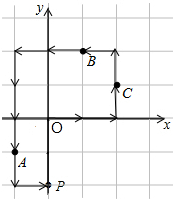
从O到C最短路径有3条:(0,0)~(1,0)~(2,0)~(2,1)、(0,0)~(1,0)~(1,1)~(2,1)、(0,0)~(0,1)~(1,1)~(2,1);
从C到B最短路径有2条:(2,1)~(2,2)~(1,2)、(2,1)~(1,1)~(1,2);
从B到A最短路径有9条:(1,2)~(0,2)~(-1,2)~(-1,1)~(-1,0)~(-1,-1),
(1,2)~(0,2)~(0,1)~(-1,1)~(-1,0)~(-1,-1),
(1,2)~(0,2)~(0,1)~(0,0)~(-1,0)~(-1,-1),
(1,2)~(0,2)~(0,1)~(0,0)~(0,-1)~(-1,-1),
(1,2)~(1,1)~(1,0)~(0,0)~(0,-1)~(-1,-1),
(1,2)~(1,1)~(1,0)~(0,0)~(0,-1)~(-1,-1),
(1,2)~(1,1)~(1,0)~(1,-1)~(0,-1)~(-1,-1),
(1,2)~(1,1)~(0,1)~(-1,1)~(-1.0)~(-1,-1),
(1,2)~(1,1)~(1,0)~(0,0)~(0,-1)~(-1,-1),
从A到P最短路径有2条:(-1,-1)~(0,-1)~(0,-2)、(-1,-1)~(-1,-2)~(0,-2);
故最短路径有3×2×9×2=108条.
点评 本题主要考查坐标与图形的性质,根据题意得出每两个点间的最短路径坐标变化是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,已知AB⊥BC,BC⊥CD,∠1=∠2,试判断BE与CF的位置关系,并说明你的理由.
如图,已知AB⊥BC,BC⊥CD,∠1=∠2,试判断BE与CF的位置关系,并说明你的理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com