

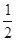 ∠ADC,∠DAM=
∠ADC,∠DAM=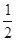 ∠BAD,由∠B=∠C=90º可得AB//CD,即可得到∠ADC+∠BAD=180º,再根据角平分线的性质求解即可.
∠BAD,由∠B=∠C=90º可得AB//CD,即可得到∠ADC+∠BAD=180º,再根据角平分线的性质求解即可.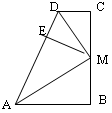
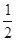 ∠ADC
∠ADC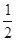 ∠BAD
∠BAD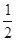 ∠ADC+
∠ADC+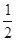 ∠BAD=
∠BAD=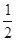 (∠ADC+∠BAD)=90º
(∠ADC+∠BAD)=90º 

 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源:不详 题型:填空题
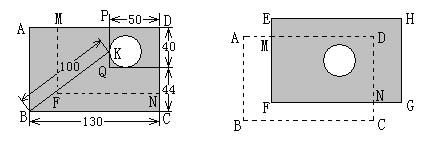
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.360° | B.540° | C.630° | D.720° |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
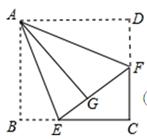
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.三角形的中线、角平分线、高线都是线段 |
| B.边数为n的多边形内角和是(n-2)×180° |
| C.有一个内角是直角的三角形是直角三角形 |
| D.三角形的一个外角大于任何一个内角 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com