
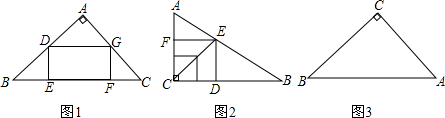
���� ��һ����1��������Rt��ABC�ڻ�һ��������PQST��ʹ�õ�P�ڱ�BC�ϣ���TS�ڱ�AB�ϣ�Ȼ������BQ���ӳ�����AC��G������G��GH��AB����BC�ڵ�H������G��GF��AB��F������H��HE��AB��E������λ�Ʊ任��֪�ı���EFGH��Ϊ��������
��2�������������������ε��������Rt��ABC�ڽ������ε������Ȼ���������������ε����ʼ����κ�������ֵ�����Rt��ABC�ڽӾ��ε����ֵ��Ȼ��ͨ���ȽϾͿɽ�����⣻
��3�������ڽӾ��ε�����������ֻ�����Rt��ABC��������Ϳɽ�����⣻
����������GH=x��Ȼ���������������ε��������CM����c��h��x��ʾ����Ȼ����Rt��EHG�����ù��ɶ�����ʾEG2��Ȼ�����ö��κ�������ֵ�����EG2����Сֵ���Ӷ��ɵõ�EG����Сֵ��
��� �⣺��һ����1����ͼ3��ʾ��������EFGH��Ϊ��������
��2����������EFGH��������
����C��CN��AB��N����GH��M����CM��GH����ͼ4��
��������EFGH�ı߳�Ϊx������GH=EH=MN=x��
�ߡ�ACB=90�㣬AC=3��BC=4��
��AB=5��CN=$\frac{AC•BC}{AB}$=$\frac{12}{5}$��
��CM=$\frac{12}{5}$-x��
���ı���EFGH�������Σ�
��GH��EF��
���CGH�ס�CAB��
��CM��GH��CN��AB��
��$\frac{CM}{CN}$=$\frac{GH}{AB}$��
��$\frac{\frac{12}{5}-x}{\frac{12}{5}}$=$\frac{x}{5}$��
��ã�x=$\frac{60}{37}$��
��S������EFGH=��$\frac{60}{37}$��2��
��������EFGH����������
����C��CN��AB��N����GH��M����CM��GH����ͼ5��
��$\frac{CM}{CN}$=$\frac{GH}{AB}$����֤����CN=$\frac{12}{5}$��AB=5��
��CM=$\frac{CN•GH}{AB}$=$\frac{\frac{12}{5}•GH}{5}$=$\frac{12}{25}$GH��
��GH=x����CM=$\frac{12}{25}$x��MN=$\frac{12}{5}$-$\frac{12}{25}$x��
��S����EFGH=GH•MN=x•��$\frac{12}{5}$-$\frac{12}{25}$x��
=-$\frac{12}{25}$��x2-5x��
=-$\frac{12}{25}$��x2-5x+$\frac{25}{4}$-$\frac{25}{4}$��
=-$\frac{12}{25}$��x-$\frac{5}{2}$��2+3��
��-$\frac{12}{25}$��0��
�൱x=$\frac{5}{2}$ʱ������EFGH�����ȡ�����ֵ�����ֵΪ3��
�ߣ�$\frac{60}{37}$��2��3��
���ڽ������ε������������������ڽӾ��ε���������3��
�ʴ𰸷ֱ�Ϊ�����ǡ�3��
��3�����ڽӾ��ε�������Ϊ3��ֱ�����������Ϊ$\frac{1}{2}$��4��3=6��
���ڽӾ��ε���������ֱ������������ı���$\frac{1}{2}$��
�ʴ�Ϊ��$\frac{1}{2}$��
������С���IJ�����ȷ��
��ͼ5��
���ı���EFGH�Ǿ��Σ�
��GH��EF��
���CGH�ס�CAB��
��CM��GH��CN��AB��
��$\frac{CM}{CN}$=$\frac{GH}{AB}$��
��AB=c��CN=h��
��CM=$\frac{CN•GH}{AB}$=$\frac{h•GH}{c}$��
��GH=x����CM=$\frac{hx}{c}$��MN=h-$\frac{hx}{c}$��
��EH=MN=h-$\frac{hx}{c}$��
��Rt��EHG��
EG2=GH2+EH2=x2+��h-$\frac{hx}{c}$��2
=$\frac{{h}^{2}+{c}^{2}}{{c}^{2}}$x2-$\frac{2{h}^{2}}{c}$x+h2��
��$\frac{{h}^{2}+{c}^{2}}{{c}^{2}}$��0��
��EG2ȡ����Сֵ��
��СֵΪ$\frac{4��\frac{{h}^{2}+{c}^{2}}{{c}^{2}}��{h}^{2}-��-\frac{2{h}^{2}}{c}��^{2}}{4��\frac{{h}^{2}+{c}^{2}}{{c}^{2}}}$=$\frac{{c}^{2}{h}^{2}}{{h}^{2}+{c}^{2}}$��
��EG����СֵΪ$\sqrt{\frac{{c}^{2}{h}^{2}}{{h}^{2}+{c}^{2}}}$=$\frac{ch\sqrt{{h}^{2}+{c}^{2}}}{{h}^{2}+{c}^{2}}$��
���� ������Ҫ������λ�Ʊ任�����������ε��ж������������ε����ʣ����������εĶ�Ӧ�ߵıȵ������Ʊȣ������κ�������ֵ�ԡ����ɶ�����֪ʶ���ڽ������Ĺ����У��õ�����Ҫ����ѧ����-�䷽���������ʽ����ֵ��������ͨ�������䷽����������⣮


 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ����ABC�У���BAC=90�㣬��D��BC���ϣ���BD=BA������B��AD�Ĵ��߽�AC�ڵ�O����OΪԲ�ģ�AOΪ�뾶��Բ��
��֪����ͼ����ABC�У���BAC=90�㣬��D��BC���ϣ���BD=BA������B��AD�Ĵ��߽�AC�ڵ�O����OΪԲ�ģ�AOΪ�뾶��Բ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
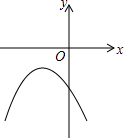 ���κ���y=ax2+bx+c��ͼ����ͼ��ʾ���������ж���ȷ���ǣ�������
���κ���y=ax2+bx+c��ͼ����ͼ��ʾ���������ж���ȷ���ǣ�������| A�� | a��0 | B�� | b��0 | C�� | c��0 | D�� | abc��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com