
数学活动﹣求重叠部分的面积
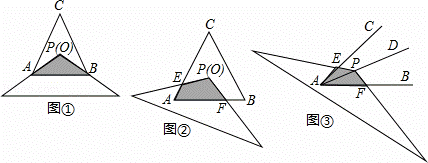
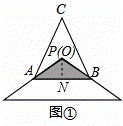
(1)问题情境:如图①,将顶角为120°的等腰三角形纸片(纸片足够大)的顶点P与等边△ABC的内心O重合,已知OA=2,则图中重叠部分△PAB的面积为 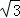 .
.
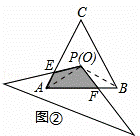
(2)探究1:在(1)的条件下,将纸片绕P点旋转至如图②所示位置,纸片两边分别与AC,AB交于点E,F,图②中重叠部分的面积与图①重叠部分的面积是否相等?如果相等,请给予证明;如果不相等,请说明理由.
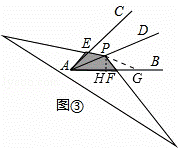
(3)探究2:如图③,若∠CAB=α(0°<α<90°),AD为∠CAB的角平分线,点P在射线AD上,且AP=2,以P为顶点的等腰三角形纸片(纸片足够大)与∠CAB的两边AC,AB分别交于点E、F,∠EPF=180°﹣α,求重叠部分的面积.(用α或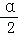 的三角函数值表示)
的三角函数值表示)
解:(1)过点O作ON⊥AB,垂足为N,如图①,
∵△ABC为等边三角形,
∴∠CAB=∠CBA=60°.
∵点O为△ABC的内心
∴∠OAB=∠CAB,∠OBA=∠CBA.
∴∠OAB=∠OBA=30°.
∴OB=OA=2.
∵ON⊥AB,
∴AN=NB,PN=1.
∴AN=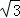
∴AB=2AN=2 .
.
∴S△OAB=AB•PN= .
.
故答案为: .
.
(2)图②中重叠部分的面积与图①重叠部分的面积相等.
证明:连接AO、BO,如图②,
由旋转可得:∠EOF=∠AOB,则∠EOA=∠FOB.
在△EOA和△FOB中,
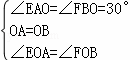
∴△EOA≌△FOB.
∴S四边形AEOF=S△OAB.
∴图②中重叠部分的面积与图①重叠部分的面积相等.
(3)在射线AB上取一点G,使得PG=PA,过点P作PH⊥AF,垂足为H,如图③,
则有AH=GH=AG.
∵∠CAB=α,AD为∠CAB的角平分线,
∴∠PAE=∠PAF=∠CAB=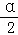 .
.
∵PG=PA,
∴∠PGA=∠PAG=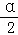 .
.
∴∠APG=180°﹣α.
∵∠EPF=180°﹣α,
∴∠EPF=∠APG.
同理可得:S四边形AEPF=S△PAG.
∵AP=2,
∴PH=2sin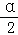 ,AH=2cos
,AH=2cos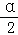 .
.
∴AG=2AH=4cos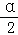 .
.
∴S△PAG=AG•PH=4sin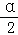 cos
cos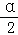 .
.
∴重叠部分得面积为:S面积=4sin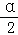 cos
cos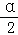 .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
小明家今年种植的“红灯”樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图象,日销售量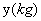 与上市时间
与上市时间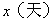 的函数关系如图1所示,樱桃价格
的函数关系如图1所示,樱桃价格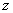 (元/
(元/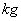 )与上市时间
)与上市时间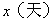 的函数关系式如图2所示。
的函数关系式如图2所示。
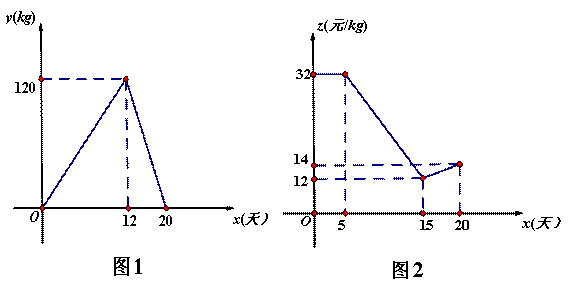 |
(1)求小明家樱桃的日销售量y与上市时间x的函数解析式。
(2)求当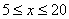 时,樱桃的价格z与上市时间x的函数解析式。
时,樱桃的价格z与上市时间x的函数解析式。
(3)求哪一天的销售金额达到最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
已知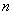 是正整数,则奇数可以用代数式
是正整数,则奇数可以用代数式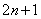 来表示.
来表示.
(1)分解因式: 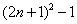 ;
;
(2)我们把所有”奇数的平方减去1”所得的数叫”白银数”,则所有”白银数”的最大公约数是多少?请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
下列事件中属于不可能事件的是( )
|
| A. | 某投篮高手投篮一次就进球 |
|
| B. | 打开电视机,正在播放世界杯足球比赛 |
|
| C. | 掷一次骰子,向上 |
|
| D. | 在一个标准大气压下,90℃的水会沸腾 |
查看答案和解析>>
科目:初中数学 来源: 题型:
某市6月份某周气温(单位:℃)为23、25、28、25、28、31、28,则这组数据的众数和中位数分别是( )
|
| A. | 25、25 | B. | 28、28 | C. | 25、28 | D. | 28、31 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com