
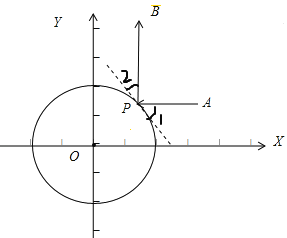
【题目】在平面直角坐标系xOy中,过⊙C上一点P作⊙C的切线l.当入射光线照射在点P处时,产生反射,且满足:反射光线与切线l的夹角和入射光线与切线l的夹角相等,点P称为反射点.规定:光线不能“穿过”⊙C,即当入射光线在⊙C外时,只在圆外进行反射;当入射光线在⊙C内时,只在圆内进行反射.特别地,圆的切线不能作为入射光线和反射光线.光线在⊙C外反射的示意图如图1所示,其中∠1=∠2.

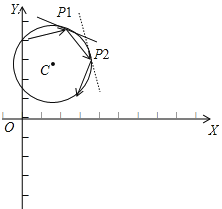
(1)自⊙C内一点出发的入射光线经⊙C第一次反射后的示意图如图2所示,P1是第1个反射点.请在图2中作出光线经⊙C第二次反射后的反射光线和反射点P3;
(2)当⊙O的半径为1时,如图3:
①第一象限内的一条入射光线平行于y轴,且自⊙O的外部照射在圆上点P处,此光线经⊙O反射后,反射光线与x轴平行,则反射光线与切线l的夹角为___________°;
②自点M(0,1)出发的入射光线,在⊙O内顺时针方向不断地反射.若第1个反射点是P1,第二个反射点是P2,以此类推,第8个反射点是P8恰好与点M重合,则第1个反射点P1的坐标为___________;
(3)如图4,点M的坐标为(0,2),⊙M的半径为1.第一象限内自点O出发的入射光线经⊙M反射后,反射光线与坐标轴无公共点,求反射点P的纵坐标的取值范围.

【答案】(1)答案见解析;(2)①45°;②(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() );(3)
);(3)![]() .
.
【解析】试题分析:(1)(2)两个问题,要根据题意,画出图象,可以解决.
(3)当反射光线平行x轴时,反射光线与坐标轴没有交点,只要求出这样的反射点,就可以解决这个问题了.
试题解析:(1)如图:
(2)①由题意:∠1=∠2,∠APB=90°,
∴∠1=45°,
∴反射光与切线的夹角为45°.
②由题意:这些反射点组成的多边形是正十二边形或正六边形,
当是正十二边形时,入射光线与反射光线夹角为150°,
∴∠AOP1=30°,
∵OP1=1,
∴P1(-![]() ,
, ![]() ).
).
当是正六边形时,易知P1(-![]() ,
, ![]() ),
),
综上所述满足条件的点P坐标为(-![]() ,
, ![]() )或(-
)或(-![]() ,
, ![]() ).
).
(3)如图:当反射光PA∥X轴时,反射光线与坐标轴没有交点,作PD⊥OC,PN⊥OM垂足分别为M,N,设OP=OC=a,PC=b,

则有 ,
,
解得b=![]() (负根已经舍弃)
(负根已经舍弃)
∵![]() ,
,
∴PD=![]() ,
,
当OP与⊙M相切时,可得点P的纵坐标为![]() ,
,
∴满足条件的反射点P的纵坐标y: ![]() ≤y<
≤y<![]() .
.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() (k为常数,k≠0)的图象经过点A(2,3).
(k为常数,k≠0)的图象经过点A(2,3).
(1)求这个函数的解析式;
(2)判断点B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由;
(3)当-3<x<-1时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象平行于y=-2x+1,且过点(2,-1),求:
(1)这个一次函数的解析式;
(2)画出该一次函数的图象:根据图象回答:当x取何值时不等式 kx+b>3.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,这是人民公园的景区示意图.以中心广场为原点,分别以正东、正北 方向为 x 轴、y 轴正方向建立平面直角坐标系,规定一个单位长度代表 100m 长.已知 各建筑物都在坐标平面网格的格点上,且东门的坐标为(400,0).

(1)请写出图中下列地点的坐标:
牡丹园 ; 游乐园 ;
(2)连接音乐台、湖心亭和望春亭这三个 地点,画出所得的三角形.然后将所 得三角形向下平移 200m,画出平移后的图形;
(3)问题(2)中湖心亭平移后的对应点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连结OE.下列结论:
BC,连结OE.下列结论:
①∠CAD=30°;②SABCD=AB·AC;③OB=AB;④OE=![]() BC,成立的结论有______.(填序号)
BC,成立的结论有______.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=![]() 在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )
在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )

A. 3 B. 4 C. 5 D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】济南市地铁1号线于2019年1月1日起正式通车,在修建过程中,技术人员不断改进技术,提高工作效率,如在打通一条长600米的隧道时,计划用若干小时完成,在实际工作过程中,每小时打通隧道长度是原计划的1.2倍,结果提前2小时完成任务.
(1)求原计划每小时打通隧道多少米?
(2)如果按照这个速度下去,后面的360米需要多少小时打通?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D为等腰直角△ABC内一点,∠ACB=90°,AD=BD,∠BAD=30°,E为AD延长线上的一点,且CE=CA,若点M在DE上,且DC=DM.则下列结论中:①∠ADB=120°;②△ADC≌△BDC;③线段DC所在的直线垂直平分线AB;④ME=BD;正确的有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,BE平分∠ABC交AD于E,CF平分∠BCD交AD于F.
(1)求证:AF=DE;
(2)若E为AD的三等分点(靠近A点),BE=8,CF=6,求直线AD与BC之间的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com