
【题目】如图,直线l1的解析表达式为:y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1,l2交于点C.
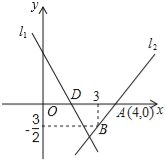
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积;
(4)在l2上存在异于点C的另一点P,使得△ADP与△ADC面积相等,求点P的坐标.
【答案】(1)D(1,0);(2)![]() ;(3)
;(3)![]() ;(4)P(6,3).
;(4)P(6,3).
【解析】
试题(1)已知l1的解析式,令y=0求出x的值即可;
(2)设l2的解析式为y=kx+b,由图联立方程组求出k,b的值;
(3)先解方程组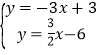 ,确定C(2,﹣3),再利用x轴上点的坐标特征确定D点坐标,然后根据三角形面积公式求解;
,确定C(2,﹣3),再利用x轴上点的坐标特征确定D点坐标,然后根据三角形面积公式求解;
(4)由于△ADP与△ADC的面积相等,根据三角形面积公式得到点P与点C到AD的距离相等,则P点的纵坐标为3,对于函数y=![]() x﹣6,计算出函数值为3所对应的自变量的值即可得到P点坐标.
x﹣6,计算出函数值为3所对应的自变量的值即可得到P点坐标.
试题解析:解:(1)∵y=﹣3x+3,
∴令y=0,得﹣3x+3=0,
解得x=1,
∴D(1,0);
(2)设直线l2的解析表达式为y=kx+b,
由图象知:x=4,y=0;x=3,y=﹣![]() ,
,
代入表达式y=kx+b,
得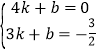 ,
,
解得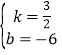 ,
,
所以直线l2的解析表达式为y=![]() x﹣6;
x﹣6;
(3)由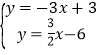 ,
,
解得![]() ,
,
∴C(2,﹣3),
∵AD=3,
∴S△ADC=![]() ×3×|﹣3|=
×3×|﹣3|=![]() ;
;
(4)因为点P与点C到AD的距离相等,
所以P点的纵坐标为3,
当y=3时,![]() x﹣6=3,解得x=6,
x﹣6=3,解得x=6,
所以P点坐标为(6,3).


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=84°.
(1)试求作一点P,使得点P到B、C两点的距离相等,并且到AC、BC两边的距离也相等(尺规作图,不写作法,保留作图痕迹).
(2)在(1)的条件下,若∠ABP=15°,求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夏季来临,商场准备购进甲、乙两种空调![]() 已知甲种空调每台进价比乙种空调多500元,用40000元购进甲种空调的数量与用30000元购进乙种空调的数量相同
已知甲种空调每台进价比乙种空调多500元,用40000元购进甲种空调的数量与用30000元购进乙种空调的数量相同![]() 请解答下列问题:
请解答下列问题:
![]() 求甲、乙两种空调每台的进价;
求甲、乙两种空调每台的进价;
![]() 若甲种空调每台售价2500元,乙种空调每台售价1800元,商场欲同时购进两种空调20台,且全部售出,请写出所获利润
若甲种空调每台售价2500元,乙种空调每台售价1800元,商场欲同时购进两种空调20台,且全部售出,请写出所获利润![]() 元
元![]() 与甲种空调
与甲种空调![]() 台
台![]() 之间的函数关系式;
之间的函数关系式;
![]() 在
在![]() 的条件下,若商场计划用不超过36000元购进空调,且甲种空调至少购进10台,并将所获得的最大利润全部用于为某敬老院购买1100元
的条件下,若商场计划用不超过36000元购进空调,且甲种空调至少购进10台,并将所获得的最大利润全部用于为某敬老院购买1100元![]() 台的A型按摩器和700元
台的A型按摩器和700元![]() 台的B型按摩器
台的B型按摩器![]() 直接写出购买按摩器的方案.
直接写出购买按摩器的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A出发,沿AB以4cm/s的速度向点B运动;同时点Q从C点出发,沿CA以3cm/s的速度向A点运动.设运动时间为x(s).
(1)当x为何值时,PQ∥BC;
(2)当△APQ与△CQB相似时,AP的长为 . ;
(3)当S△BCQ:S△ABC=1:3,求S△APQ:S△ABQ的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,⊙O是△ABC的外接圆, ![]() ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.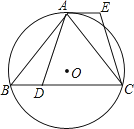
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.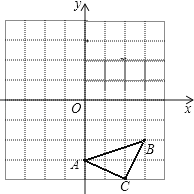
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2 , 使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车2015年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.
(1)求今年6月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A、B两种型号车的进货和销售价格如表:
A型车 | B型车 | |
进货价格(元/辆) | 1100 | 1400 |
销售价格(元/辆) | 今年的销售价格 | 2400 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,坐标平面上,二次函数y=﹣x2+4x﹣k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知实数![]() +1的整数部分为m,小数部分为n.
+1的整数部分为m,小数部分为n.
(1)求m,n的值;
(2)在平面直角坐标系中,试判断点(m﹣1,n﹣1)位于第几象限;
(3)若m,n+1为一个直角三角形的斜边与一条直角边的长,求这个直角三角形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com