
如图,等腰三角形ABC中,AC=BC=3,AB=4.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
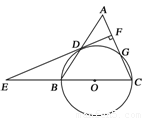
(1)求证:直线EF是⊙O的切线;
(2)连接BG,求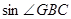 的值.
的值.
(1)连接OD,根据圆的基本性质可得∠OBD=∠ODB,再由AC=BC可得∠OBD=∠A,即可得到∠ODB=∠A,从而可得OD//AC,再结合DF⊥AC即可证得结论;(2)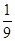
【解析】
试题分析:(1)连接OD,根据圆的基本性质可得∠OBD=∠ODB,再由AC=BC可得∠OBD=∠A,即可得到∠ODB=∠A,从而可得OD//AC,再结合DF⊥AC即可证得结论;
(2)设CG=x,BC=3,CG=x,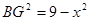 AG=3-x,AB=4,再根据勾股定理即可列方程求解.
AG=3-x,AB=4,再根据勾股定理即可列方程求解.
(1)连接OD
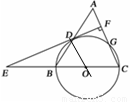
∵OB=OD
∴∠OBD=∠ODB
∵AC=BC
∴∠OBD=∠A
∴∠ODB=∠A
∴OD//AC
∴∠EDO=∠EFC=90°
∴EF为切线;
(2) 设CG=x,BC=3,CG=x,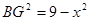 AG=3-x,AB=4
AG=3-x,AB=4
由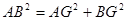 可得
可得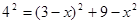 ,解得x=
,解得x=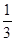 ,
,
则sin∠GBC=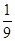 .
.
考点:圆的基本性质,等腰三角形的性质,平行线的判定和性质,切线的判定,勾股定理
点评:在证明切线的问题中,一般先连接切点与圆心,再证垂直.


科目:初中数学 来源: 题型:
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| a |
| b |
 (1)他们的说法合理吗?为什么?
(1)他们的说法合理吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:
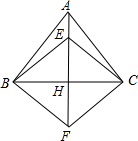 如图,等腰三角形ABC中,AB=AC,AH垂直BC,点E是AH上一点,延长AH至点F,使FH=EH,
如图,等腰三角形ABC中,AB=AC,AH垂直BC,点E是AH上一点,延长AH至点F,使FH=EH,查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,等腰三角形ABC(AB=AC)的底角为50°,绕点A逆时针旋转一定角度后得△AB′C′,那么△AB′C′绕点A旋转
如图,等腰三角形ABC(AB=AC)的底角为50°,绕点A逆时针旋转一定角度后得△AB′C′,那么△AB′C′绕点A旋转查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com