
 absinC列出等式
absinC列出等式 |PA|•|PB|sin∠APB=
|PA|•|PB|sin∠APB= |PM|•|PN|sin∠MPN.即
|PM|•|PN|sin∠MPN.即 =
=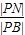 ;再根据两点间的距离公式求得
;再根据两点间的距离公式求得 =
=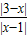 ,即(3-x)2=|x2-1|,解得x=
,即(3-x)2=|x2-1|,解得x= .易求y的值.
.易求y的值. 解:∵点B与点A(-1,1)关于原点O对称,∴点B的坐标为(1,-1).
解:∵点B与点A(-1,1)关于原点O对称,∴点B的坐标为(1,-1). |PA|•|PB|sin∠APB=
|PA|•|PB|sin∠APB= |PM|•|PN|sin∠MPN.
|PM|•|PN|sin∠MPN. =
=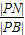 ,
, =
= ,即(3-x)2=|x2-1|,解得x=
,即(3-x)2=|x2-1|,解得x= .
. ,
, ,±
,±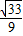 ).
). ,±
,±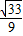 ).
).

科目:初中数学 来源: 题型:
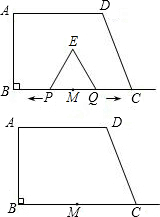 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=6,BC=8,AB=3
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=6,BC=8,AB=3| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
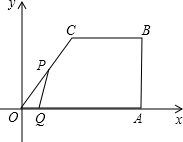 .
.查看答案和解析>>
科目:初中数学 来源: 题型:
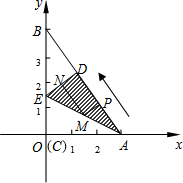 AB边上,记为D点,AE为折痕,E在y轴上.
AB边上,记为D点,AE为折痕,E在y轴上.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 5 |
| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 四跳落点于P4,P4与P3关于竹竿l成轴对称;以此跃下去,若每25跳可以休息一次.
四跳落点于P4,P4与P3关于竹竿l成轴对称;以此跃下去,若每25跳可以休息一次.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com