
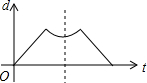
 设圆、等腰直角三角形、正方形和等腰三角形边界上的一个定点为Q(如四个选项中的图形),动点P从点Q出发,在其边界上按顺时针方向匀速运动一周后又回到起点Q.设点P运动的时间是t,点P和点Q之间的距离是d,如图是d与t之间函数关系的大致图象,则该图形可能是( )
设圆、等腰直角三角形、正方形和等腰三角形边界上的一个定点为Q(如四个选项中的图形),动点P从点Q出发,在其边界上按顺时针方向匀速运动一周后又回到起点Q.设点P运动的时间是t,点P和点Q之间的距离是d,如图是d与t之间函数关系的大致图象,则该图形可能是( )| A. |  | B. | 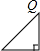 | C. | 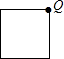 | D. | 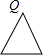 |
分析 根据圆,等腰直角三角形,正方形,等边三角形性质,分析得到d随t的增大而变化关系,然后选择答案即可.
解答 解:A、圆,随着点P运动,d的长度先变速增加至PQ为直径,然后再变速减小至点P回到点Q,题干图象不符合;
B、等腰直角三角形,点P在一开始沿直角边运动时,d的长度为直线变化增大,
沿另一条直角边运动时,设直角边长为a,则d=$\sqrt{{a}^{2}+(t-a)^{2}}$(a<t<2a),
在斜边运动时,d的长度为直线变化减小,且长度与直角边不相等,题干图象不符合;
C、正方形,点P在开始与结束的两边上直线变化,在另两边上,先变速增加至∠Q的对角顶点,再变速减小至另一顶点,题干图象不符合;
D、等边三角形,点P在开始与结束的两边上直线变化,
在点Q的对边上时,设等边三角形的边长为a,
则y=$\sqrt{(\frac{\sqrt{3}}{2}a)^{2}+(\frac{3}{2}a-t)^{2}}$(a<x<2a),符合题干图象;
故选:D.
点评 本题考查了动点问题函数图象,熟练掌握圆,等腰直角三角形,正方形以及等边三角形的性质,理清点P在各边时d的长度的变化情况是解题的关键.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 5 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
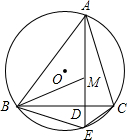 如图,点M是△ABC的内心,AM的延长线交边BC于点D,交△ABC外接圆⊙O于点E,连接BE、CE.
如图,点M是△ABC的内心,AM的延长线交边BC于点D,交△ABC外接圆⊙O于点E,连接BE、CE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
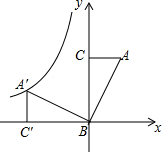 如图,Rt△ABC的一个顶点B在原点,BC在y轴上,直角边AC=1,BC=2,把Rt△ABC绕点B逆时针旋转90°,顶点A的对应点为A′.若反比例函数y=$\frac{m}{x}$的图象经过点A′,则m的值为( )
如图,Rt△ABC的一个顶点B在原点,BC在y轴上,直角边AC=1,BC=2,把Rt△ABC绕点B逆时针旋转90°,顶点A的对应点为A′.若反比例函数y=$\frac{m}{x}$的图象经过点A′,则m的值为( )| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
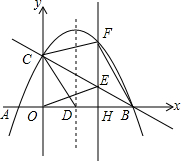 如图,抛物线y=-$\frac{1}{2}$x2+mx+2与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴直线x=$\frac{3}{2}$交x轴于点D.
如图,抛物线y=-$\frac{1}{2}$x2+mx+2与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴直线x=$\frac{3}{2}$交x轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 居民户数 | 1 | 5 | 3 | 1 |
| 月用水量(米3/户) | 10 | 15 | 20 | 25 |
| A. | 15 | B. | 17.5 | C. | 20 | D. | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com