

���� ��1���������⣬ֱ�ӽ���PMN��������Ӽ��ɵó���t�ı���ʽ���á�NPBΪ���������Σ��ɵõ�NB=NP=NM=t+1����NB=CB-CM-MN����ʽ��������5-2t=t+1����֮���ɵó�t��
��2�����ص�����Ϊһ��С�ȱ������Σ�������ֱ�ó��ױ����Ӧ�ĸ��ɵó��ص����ֵ������
��3��������⣬��֪��������������Ե�AΪԲ�ġ�tcmΪ�뾶�ġ�A��MN���ڵ�ֱ�����У��ڡ�A��MN���ڵ�ֱ�����У��ۡ�A��PN���ڵ�ֱ�����У��ֱ��������ߵ������Լ����ɶ��������ɵó����������Ӧ��tֵ��
��� 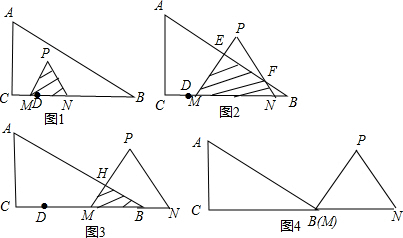 �⣺��1����PMN�ı߳�MN=CN-CM=��CD+DN��-CM=��1+2t��-t=��t+1��cm��
�⣺��1����PMN�ı߳�MN=CN-CM=��CD+DN��-CM=��1+2t��-t=��t+1��cm��
�ߵ�tΪijֵʱ����P����AB�ϣ�������PMN�ǵȱ������Σ�
��NB=NP=MN=t+1����PND=60�㣬
���PNB=120�㣬��PNB=30�㣬
���PNB����������
��Q=NB=CB-CM-PMN=6-t-��t+1��=5-2t��
��5-2t=t+1��
��ã�t=$\frac{4}{3}$s��
�ʴ�Ϊ��t+1��$\frac{4}{3}$��
��2����Ϊ����������ٵ�0��t��$\frac{4}{3}$ʱ����ͼ1���ص������ǡ�PMN��
�ߡ�PMN�ı߳�Ϊt+1��
���Ϊ$\frac{\sqrt{3}}{2}$��t+1��cm��
��S=$\frac{1}{2}$����t+1����$\frac{\sqrt{3}}{2}$��t+1��=$\frac{\sqrt{3}}{4}$��t+1��2��
�ڵ�$\frac{4}{3}$��t��$\frac{5}{2}$ʱ����ͼ2���ص�����Ϊ�ı���MNFE��
�ߡ�B=30�㣬�ҡ�PMNΪ�ȱ������Σ�
���PMN=��P=60�㣬
���PEF=90�㣬��MB=BC-CM=6-t����PFE=30�㣬
��PE=$\frac{1}{2}$��6-t����
��EP=PM-NF=��t+1��-$\frac{1}{2}$��6-t��=$\frac{1}{2}$��3t-4����
��EF=M=EP•tan60��=$\frac{\sqrt{3}}{2}$��3t-4����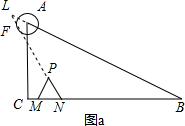
��S=$\frac{\sqrt{3}}{4}$��t+1��2-$\frac{\sqrt{3}}{8}$��3t-4��2
=-$\frac{7\sqrt{3}}{8}$t2+$\frac{7\sqrt{3}}{2}$t-$\frac{7\sqrt{3}}{4}$
=-$\frac{7\sqrt{3}}{8}$��t-2��2+$\frac{7\sqrt{3}}{4}$��
�۵�$\frac{5}{2}$��t��6ʱ����ͼ3��ͬ���ɵ�y=$\frac{\sqrt{3}}{8}$��6-t��2��
�ܵ�t��6ʱ����ͼ4����ʱy=0��
��3����һ����ͼa��
��A��PN���ڵ�ֱ������ʱ���е�ΪF��F��PN���ӳ����ϣ�AB��FN����L�㣬
AF=t���õ�AL=2t��
NB=5-2t���õ�BL=$\sqrt{3}$��5-2t����
AB=4$\sqrt{3}$=BL-AL=$\sqrt{3}$��5-2t��-2t��
�õ�t=$\frac{3-\sqrt{3}}{4}$��
��t=$\frac{3-\sqrt{3}}{4}$��
��ͼb����FP��AB��E��
�ߡ�A�뾶=AF=t����AE=2t��NE=NB=5-2t��BE=$\sqrt{3}$��5-2t����
AB=4$\sqrt{3}$=BE+AE=$\sqrt{3}$��5-2t��+2t��
��t=$\frac{3+\sqrt{3}}{4}$��
��������ͼc��
����A��MN���ڵ�ֱ������ʱ��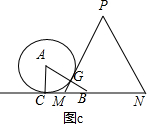
��AC��MN���ڵ�ֱ�ߣ�
���A�뾶=AC=t=2$\sqrt{3}$��
��ʱ������AB��PM�ཻ��G��
��AG=��A�뾶=2$\sqrt{3}$��
��BM=4$\sqrt{3}$-2$\sqrt{3}$=2$\sqrt{3}$��
���MGB=90�㣬
���A Ҳͬʱ��PM���У�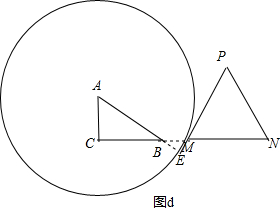
��������ͼd��
��A��PM���ڵ�ֱ������ʱ���е�ΪE����֪����E��AB�ӳ����ϣ�
��Rt��MBE�У���ABC=30�㣬��AE=t��BE=AE-AB=t-4$\sqrt{3}$��б��MB=CM-BC=t-6��
����$\frac{\sqrt{3}}{2}$MB=BE����$\frac{\sqrt{3}}{2}$��t-6��=t-4$\sqrt{3}$��
�õ�t=4$\sqrt{3}$+6��
��������������A��QR���ڵ�ֱ������ʱ��t=$\frac{3-\sqrt{3}}{4}$��t=$\frac{3+\sqrt{3}}{4}$����
����A��PQ���ڵ�ֱ������ʱ��t=2$\sqrt{3}$��
����A��PR���ڵ�ֱ�����У�t=4$\sqrt{3}$+6��
���� ���⿼����Բ���������ʣ�����ֱ�������ε�֪ʶ���������ߵ����������м������֤�����һ�����ڿ��������⣬��Ҫ��������������ʵ�ʵ��Ӧ�ã�������һ����̬�����⣬�ۺ��Խ�ǿ����һ�����Ѷȣ�


 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д� �����ܿ����ϵ�д�
�����ܿ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | M=N | B�� | M��N | C�� | M��N | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m=1 | B�� | m��1 | C�� | m��1 | D�� | m��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
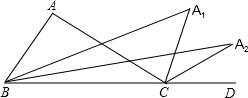 ��ͼ����ABC�У���A=���㣬�ӳ�BC��D����ABC���ACD��ƽ�����ཻ�ڵ�A1����A1BC���A1CD��ƽ�����ཻ�ڵ�A2���������ƣ���An-1BC���An-1CD��ƽ�����ཻ�ڵ�An�����An�Ķ���Ϊ��������
��ͼ����ABC�У���A=���㣬�ӳ�BC��D����ABC���ACD��ƽ�����ཻ�ڵ�A1����A1BC���A1CD��ƽ�����ཻ�ڵ�A2���������ƣ���An-1BC���An-1CD��ƽ�����ཻ�ڵ�An�����An�Ķ���Ϊ��������| A�� | ${��{\frac{��}{n}}����}$ | B�� | ${��{\frac{��}{2n}}����}$ | C�� | ${��{\frac{��}{2^n}}����}$ | D�� | ${��{\frac{��}{{{2^{n+1}}}}}����}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
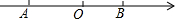 ��ͼ����֪��A�������϶�Ӧ����Ϊa����B��Ӧ����Ϊb����a��b����|a+3|+��b-2��2=0��
��ͼ����֪��A�������϶�Ӧ����Ϊa����B��Ӧ����Ϊb����a��b����|a+3|+��b-2��2=0���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com