
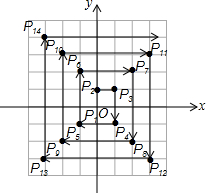
 如图,在平面直角坐标系中,每个最小方格的边长均为1个单位长,P1,P2,P3,…,均在格点上,其顺序按图中“→”方向排列,如:P1(0,0),P2(0,1),P3(1,1),P4(1,-1),P5(-1,-1),P6(-1,2)…根据这个规律,点P2017的坐标为(-504,-504).
如图,在平面直角坐标系中,每个最小方格的边长均为1个单位长,P1,P2,P3,…,均在格点上,其顺序按图中“→”方向排列,如:P1(0,0),P2(0,1),P3(1,1),P4(1,-1),P5(-1,-1),P6(-1,2)…根据这个规律,点P2017的坐标为(-504,-504). 分析 根据各个点的位置关系,可得出下标为4的倍数的点在第四象限的角平分线上,被4除余1的点在第三象限的角平分线上,被4除余2的点在第二象限的角平分线上,被4除余3的点在第一象限的角平分线上,点P2017的在第三象限的角平分线上,且横纵坐标的绝对值=(2017-1)÷4,再根据第三项象限内点的符号得出答案即可.
解答 解:由规律可得,(2017-1)÷4,
∴点P2017的在第三象限的角平分线上,
∵点P5(-1,-1),
∴点P2017(-504,-504).
故答案为:(-504,-504).
点评 本题考查了规律型:点的坐标,是一个阅读理解,猜想规律的题目,解答此题的关键是首先确定点所在的大致位置,所在正方形,然后就可以进一步推得点的坐标.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
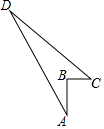 如图,四边形ABCD中,AB=4cm,BC=3cm,CD=12cm,DA=13cm,且∠ABC=90°,则四边形ABCD的面积为( )
如图,四边形ABCD中,AB=4cm,BC=3cm,CD=12cm,DA=13cm,且∠ABC=90°,则四边形ABCD的面积为( )| A. | 6cm2 | B. | 30cm2 | C. | 24cm2 | D. | 36cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
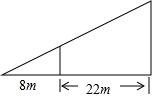 如图,小明用长为3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m,竹竿与旗杆相距22m,则旗杆的高为( )
如图,小明用长为3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m,竹竿与旗杆相距22m,则旗杆的高为( )| A. | 12m | B. | 9.6m | C. | 8m | D. | 6.6m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 脸谱是中国戏曲男演员脸部的彩色化妆.这种脸部化妆主要用于净(花脸)和丑(小丑),表现人物的性格和特征.现有四张脸谱,如图所示:有两张相同的表现忠勇侠义的净角姜维,有一张表现直爽刚毅的净角包拯,有一张表现阴险奸诈的丑角夏侯婴.
脸谱是中国戏曲男演员脸部的彩色化妆.这种脸部化妆主要用于净(花脸)和丑(小丑),表现人物的性格和特征.现有四张脸谱,如图所示:有两张相同的表现忠勇侠义的净角姜维,有一张表现直爽刚毅的净角包拯,有一张表现阴险奸诈的丑角夏侯婴.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
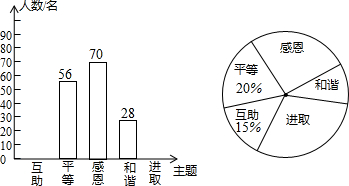
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
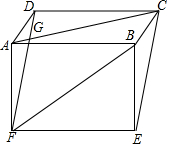 已知:如图,在平行四边形ABCD和矩形ABEF中,AC与DF相交于点G.
已知:如图,在平行四边形ABCD和矩形ABEF中,AC与DF相交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com