
分析 (1)根据根与系数的关系得a+b=c+6,ab=6c+18,则(a+b)2=(c+6)2,整理可得a2+b2=c2,根据勾股定理的逆定理可判断△ABC为直角三角形;
(2)根据根的判别式的意义得到(c-6)2≥72,而c>6,利用不等式的性质可解得c≥6+6$\sqrt{2}$,再根据三角形面积公式得到△ABC的面积=$\frac{1}{2}$•ab=3c+9,所以c=6+6$\sqrt{2}$时,△ABC的面积最小,然后把c的值代入3c+9中计算即可.
解答 解:(1)根据题意得a+b=c+6,ab=6c+18,
∵(a+b)2=(c+6)2,
∴a2+b2+2ab=c2+12c+36,
∴a2+b2=c2,
∴△ABC为直角三角形,∠C=90°;
(2)∵△=(c+6)2-4(6c+18)≥0,
(c-6)2≥72,
而c>6,
∴c≥6+6$\sqrt{2}$,
∵△ABC的面积=$\frac{1}{2}$•ab=$\frac{1}{2}$•(6c+18)=3c+9,
∴c=6+6$\sqrt{2}$时,△ABC的面积最小,最小值=3(6+6$\sqrt{2}$)+9=27+18$\sqrt{2}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式和勾股定理的逆定理.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 3.5 | C. | 4 | D. | 4.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
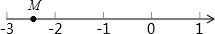 在数轴上,点M的位置如图所示,设点M表示有理数m,点P表示m的相反数,点Q表示m的倒数,点N表示m的绝对值,点R表示m的平方.则这些点中,一定与M位于原点同侧的点是( )
在数轴上,点M的位置如图所示,设点M表示有理数m,点P表示m的相反数,点Q表示m的倒数,点N表示m的绝对值,点R表示m的平方.则这些点中,一定与M位于原点同侧的点是( )| A. | 点P | B. | 点Q | C. | 点N | D. | 点R |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
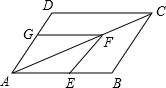 如图,平行四边形ABCD∽平行四边形AEFG,若平行四边形ABCD周长为60cm,AF=12cm,FC=8cm,则平行四边形AEFG的周长是36cm.
如图,平行四边形ABCD∽平行四边形AEFG,若平行四边形ABCD周长为60cm,AF=12cm,FC=8cm,则平行四边形AEFG的周长是36cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com