
【题目】如图,∠AOC与∠BOD都是直角,则下列说法正确的是( )
①若∠COD=30°,则∠AOB=150°
②∠BOC=∠AOB﹣∠BOD
③∠AOD=∠BOC
④∠AOB与∠DOC的和不变
⑤∠AOB与∠DOC的和随∠DOC的变小而增大.
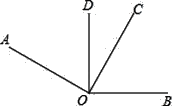
A. ①③④ B. ①②③④ C. ①③⑤ D. ①②③⑤
 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,OD垂直于弦AC于点E,且交⊙O于点D,F是BA延长线上一点,若∠CDB=∠BFD. 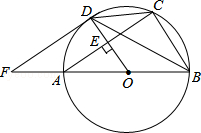
(1)求证:FD是⊙O的一条切线;
(2)若AB=10,AC=8,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是假命题的是( )
A. 在△ABC中,若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
B. 在△ABC中,若a2=(b+c) (b-c),则△ABC是直角三角形
C. 在△ABC中,若∠B=∠C=∠A,则△ABC是直角三角形
D. 在△ABC中,若a:b:c=5:4:3,则△ABC是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料.
我们知道,1+2+3+…+n=![]() ,那么12+22+32+…+n2结果等于多少呢?
,那么12+22+32+…+n2结果等于多少呢?
在图1所示三角形数阵中,第1行圆圈中的数为1,即12,第2行两个圆圈中数的和为2+2,即22,…;第n行n个圆圈中数的和为n+n+n+…+n,即n2.这样,该三角形数阵中共有![]() 个圆圈,所有圆圈中数的和为12+22+32+…+n2.
个圆圈,所有圆圈中数的和为12+22+32+…+n2.
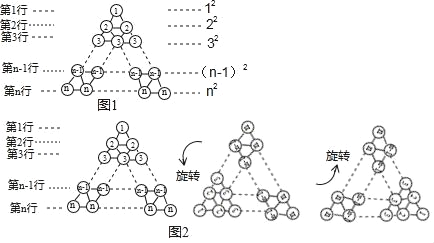
(规律探究)
将三角形数阵经两次旋转可得如图2所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第n﹣1行的第一个圆圈中的数分别为n﹣1,2,n),发现每个位置上三个圆圈中数的和均为 ,由此可得,这三个三角形数阵所有圆圈中数的总和为3(12+22+32+…+n2)= ,因此,12+22+32+…+n2= .
(解决问题)
根据以上发现,计算:![]() 的结果为 .
的结果为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长方形纸片按如图所示的方式折叠,BC、BD为折痕.若∠ABC=25°,则∠DBE的度数为( )
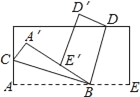
A. 50° B. 65° C. 45° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,则下列结论: ①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个互异实根.
其中正确结论的个数是( )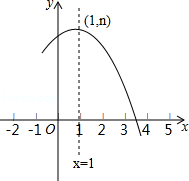
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分6分)某公司调查某中学学生对其环保产品的了解情况,随机抽取该校部分学生进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为A、B、C、D.根据调查结果绘制了如下尚不完整的统计图. 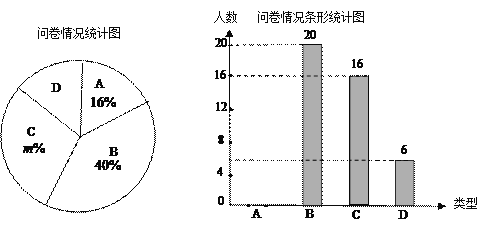
(1)本次问卷共随机调查了 名学生,扇形统计图中m= .
(2)请根据数据信息补全条形统计图;
(3)若该校有1000名学生,估计选择“非常了解”、“比较了解”共约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“汉字听写大赛”活动,为了解学生的参与情况,在该校随机抽取了四个班级学生进行调查,将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图,请根据图中的信息,解答下列问题: 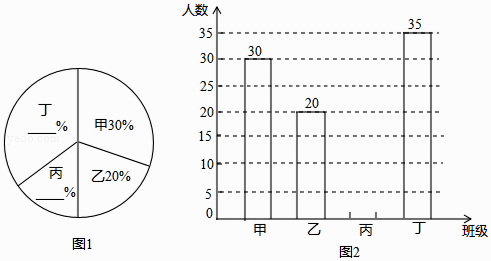
(1)这四个班参与大赛的学生共人;
(2)请你补全两幅统计图;
(3)求图1中甲班所对应的扇形圆心角的度数;
(4)若四个班级的学生总数是160人,全校共2000人,请你估计全校的学生中参与这次活动的大约有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com