
【题目】如图,已知AC为正方形ABCD的对角线,点P是平面内不与点A,B重合的任意一点,连接AP,将线段AP绕点P顺时针旋转![]() 得到线段PE,连接AE,BP,CE.
得到线段PE,连接AE,BP,CE.
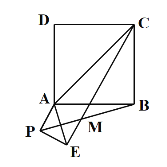
(1)求证:![]() ;
;
(2)当线段BP与CE相交时,设交点为M,求![]() 的值以及
的值以及![]() 的度数;
的度数;
(3)若正方形ABCD的边长为3,![]() ,当点P,C,E在同一直线上时,求线段BP的长.
,当点P,C,E在同一直线上时,求线段BP的长.
【答案】(1)见解析;(2)![]() ,
,![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据题意可知![]() 为等腰直角三角形,根据等腰直角三角形性质和正方形的性质可得
为等腰直角三角形,根据等腰直角三角形性质和正方形的性质可得![]() ,
,![]() ,然后利用两组对应边成比例及其夹角相等的两个三角形相似即可证出
,然后利用两组对应边成比例及其夹角相等的两个三角形相似即可证出![]() ;
;
(2)利用两组对应边成比例及其夹角相等的两个三角形相似,即可证出![]() ,利用相似三角形的性质即可求出
,利用相似三角形的性质即可求出![]() 的值,
的值,![]() ,然后利用三角形的内角和即可求出
,然后利用三角形的内角和即可求出![]() ;
;
(3)根据点P、C、E的相对位置分类讨论:①当点E在线段CP上时,利用勾股定理求出PC的长,从而求出CE的长,再根据(2)的结论即可求出BP;②当点P在线段CE上时,原理同上.
解:(1)∵线段AP绕点P顺时针旋转![]() 得到线段PE
得到线段PE
∴![]() 为等腰直角三角形
为等腰直角三角形
∴![]() ,
,![]()
∵在正方形ABCD中,![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
∴![]()
(2)由(1)知![]()
∴![]()
即![]()
又∵![]()
∴![]()
∴![]() ,
,![]()
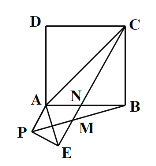
又∵![]()
∴![]()
(3)①如下图所示,当点E在线段CP上时
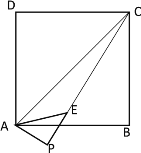
∵在正方形ABCD中,∠![]() ,
,![]()
∴![]()
∴在![]() 中,
中,![]()
∴![]()
∵由(2)知![]() 且
且![]()
∴![]() ;
;
②如下图所示,当点P在线段CE上时
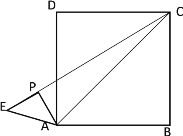
由①得![]() ,
,![]()
∴![]()
由(2)知![]() 且
且![]()
∴![]() ;
;
综上所述:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】![]() 是等边三角形,点P在
是等边三角形,点P在![]() 的延长线上,以P为中心,将线段
的延长线上,以P为中心,将线段![]() 逆时针旋转n°(
逆时针旋转n°(![]() )得线段
)得线段![]() ,连接
,连接![]() ,
,![]() .
.


(1)如图,若![]() ,画出当
,画出当![]() 时的图形,并写出此时n的值;
时的图形,并写出此时n的值;
(2)M为线段![]() 的中点,连接
的中点,连接![]() .写出一个n的值,使得对于
.写出一个n的值,使得对于![]() 延长线上任意一点P,总有
延长线上任意一点P,总有![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
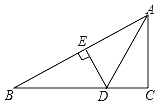
【题目】如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于点D,DE恰好是AB的垂直平分线,垂足为E.若BC=6,则AB的长为( )
A.3![]() B.4
B.4![]() C.8D.10
C.8D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣![]() x2+bx+c与x轴交于原点O和点A(6,0),抛物线的顶点为B.
x2+bx+c与x轴交于原点O和点A(6,0),抛物线的顶点为B.
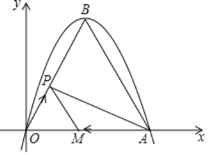
(1)求该抛物线的解析式和顶点B的坐标;
(2)若动点P从原点O出发,以每秒1个长度单位的速度沿线段OB运动,设点P运动的时间为t(s).问当t为何值时,△OPA是直角三角形?
(3)若同时有一动点M从点A出发,以2个长度单位的速度沿线段AO运动,当P、M其中一个点停止运动时另一个点也随之停止运动.设它们的运动时间为t(s),连接MP,当t为何值时,四边形ABPM的面积最小?并求此最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像相交于A,B两点,与x轴相交于点C,连接OB,且
的图像相交于A,B两点,与x轴相交于点C,连接OB,且![]() 的面积为
的面积为![]() .
.
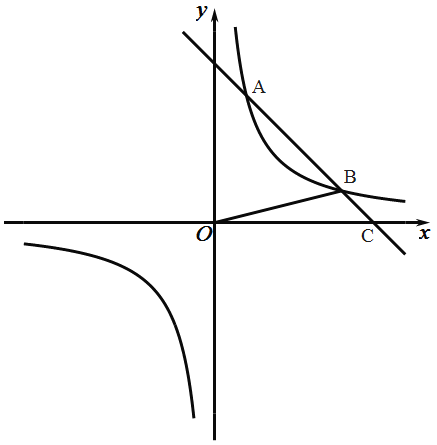
(1)求反比例函数的表达式;
(2)将直线AB向下平移,若平移后的直线与反比例函数的图像只有一个交点,试说明直线AB向下平移了几个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是![]() 的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且
的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且![]() ,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.
,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.

(1)求证:BD是⊙O的切线;(2)当OB=2时,求BH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+6与反比例函数![]() 的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(1)求m的值和反比例函数的表达式;
(2)观察图象,直接写出当x>0时,不等式2x+6-![]() <0的解集;
<0的解集;
(3)当n为何值时,△BMN的面积最大?最大值是多少?
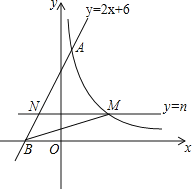
查看答案和解析>>
科目:初中数学 来源: 题型:
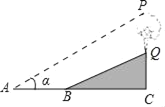
【题目】如图,已知斜坡BQ的坡度i=1:2.4,坡长BQ=13米,在斜坡BQ上有一棵银杏树PQ,小李在A处测得树顶P的仰角为α,测得水平距离AB=8米.若tanα=0.75,点A,B,P,Q在同一平面上,PQ⊥AB于点C,则银杏树PQ的高度为_____米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com