
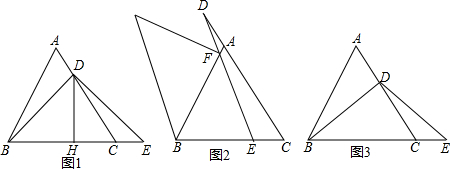
分析 (1)①证明:如图1中,作DK∥BC交AB于K.只要证明△DKB≌△ECD即可解决问题;
②只要证明△DBH是等腰直角三角形即可解决问题;
(2)如图2中,作BN∥DE,DN∥EB,则四边形BEDN是平行四边形,作BH⊥DE于H,FM⊥BN于M.连接FN.想办法证明△BFN是等腰直角三角形即可解决问题;
(3)如图3中,作DH∥BC交AB于H.由(1)可知△DHB≌△ECD,推出S△BDH=S△CDE,推出S△BDE=S四边形DHBC,由DH∥BC,可得△ADH∽△ACB,推出$\frac{{S}_{△ADH}}{{S}_{△ACB}}$=($\frac{AD}{AC}$)2,求出△ADH的面积即可解决问题;
解答 (1)①证明:如图1中,作DK∥BC交AB于K.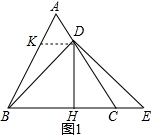
∵△ABC是等边三角形,
∴AB=AC,∠ABC=∠ACB=60°,
∴∠AKD=∠ABC=60°,∠ADK=∠ACB=60°,
∴△ADK是等边三角形,
∴AD=DK=AK=CE,
∴BK=CD,∵∠DKB=∠DCE=120°,
∴△DKB≌△ECD,
∴BD=ED.
②如图1中,∵BD=DE,∠BDE=90°,
∴∠DBH=45°,
∵DH⊥BC,
∴∠DHB=90°,
∴△DHB是等腰直角三角形,
∴BD=$\sqrt{2}$DH.
(2)证明:如图2中,作BN∥DE,DN∥EB,则四边形BEDN是平行四边形,作BH⊥DE于H,FM⊥BN于M.连接FN.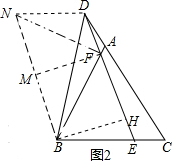
同法可证:BD=DE,
∴BN=DE=BD,
∵∠EDC=15°,∠C=60°,
∴∠DEB=∠DBE=75°,
∴∠BDE=30°,
在Rt⊥BDH中,BH=$\frac{1}{2}$BD,
∵∠FBE=60°,
∴∠BFE=180°-60°-75°=45°,
∴BH=FH,易证四边形BHFM是正方形,
∴BH=FH=BM=FM=$\frac{1}{2}$BN,
∴BM=MN=FM,
∴△BFN是等腰直角三角形,
∴BN=$\sqrt{2}$BF,
∴BD=$\sqrt{2}$BF.
(3)解:如图3中,作DH∥BC交AB于H.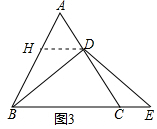
由(1)可知△DHB≌△ECD,
∴S△BDH=S△CDE,
∴S△BDE=S四边形DHBC,
∵DH∥BC,
∴△ADH∽△ACB,
∴$\frac{{S}_{△ADH}}{{S}_{△ACB}}$=($\frac{AD}{AC}$)2,
∵CD=2CE,AD=CE,
∴CD=2AD,
∴AD:AC=1:3,
∴$\frac{{S}_{△ADH}}{{S}_{△ACB}}$=($\frac{AD}{AC}$)2=$\frac{1}{9}$,∵S△ACB=8,
∴S△ADH=$\frac{8}{9}$,
∴S△BDE=S四边形DHBC=8-$\frac{8}{9}$=$\frac{64}{9}$.
故答案为$\frac{64}{9}$.
点评 本题考查三角形综合题、等边三角形的判定和性质、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{22}{7}$,$\sqrt{6}$ | |
| B. | $\frac{π}{5}$,1.010010001…(两个“1”之间依次多一个“0”) | |
| C. | $\sqrt{4}$,3.14159 | |
| D. | 2π,$-\root{3}{27}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com