
【题目】如图,点O为原点,A. B为数轴上两点,AB=15,且OA:OB=2.
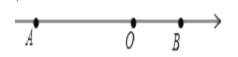
(1)A、B对应的数分别为___、___;
(2)点A. B分别以4个单位/秒和3个单位/秒的速度相向而行,则几秒后A. B相距1个单位长度?
(3)点A. B以(2)中的速度同时向右运动,点P从原点O以7个单位/秒的速度向右运动,是否存在常数m,使得4AP+3OBmOP为定值,若存在请求出m值以及这个定值;若不存在,请说明理由。
【答案】(1)A、B对应的数分别为10、5;(2)2或![]() 秒;(3)当m=3时,4AP+3OBmOP为定值55.
秒;(3)当m=3时,4AP+3OBmOP为定值55.
【解析】
(1)根据题意求出OA、OB的长,根据数轴的性质解答;
(2)分点A在点B的左侧、点A在点B的右侧两种情况,列方程解答;
(3)根据题意列出关系式,根据定值的确定方法求出m即可.
(1)设OA=2x,则OB=x,
由题意得,2x+x=15,
解得,x=5,
则OA=10、OB=5,
∴A、B对应的数分别为10、5,
故答案为:10;5;
(2)设x秒后A. B相距1个单位长度,
当点A在点B的左侧时,4x+3x=151,
解得,x=2,
当点A在点B的右侧时,4x+3x=15+1,
解得,x=![]() ,
,
答:2或![]() 秒后A. B相距1个单位长度;
秒后A. B相距1个单位长度;
(3)设t秒后4AP+3OBmOP为定值,
由题意得,4AP+3OBmOP=4×[7t(4t10)]+3(5+3t)7mt
=(217m)t+55,
∴当m=3时,4AP+3OBmOP为定值55.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
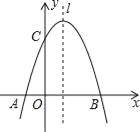
【题目】如图,已知抛物线y=![]() +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
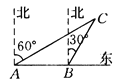
【题目】如图所示,一艘渔船正以30海里/时的速度由西向东追赶鱼群,自A处经半小时到达B处,在A处看见小岛C在船的北偏东60°的方向上,在B处看见小岛C在船的北偏东30°的方向上,已知以小岛C为中心周围10海里以内为我军导弹部队军事演习的着弹危险区,则这艘船继续向东追赶鱼群,是否有进入危险区域的可能?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线过A(-1,0),B(3,0)两点,与y轴交于C点,且BC=3![]() ,则这条抛物线的解析式为 ( )
,则这条抛物线的解析式为 ( )
A. y=-x2+2x+3 B. y=x2-2x-3
C. y=x2+2x―3或y=-x2+2x+3 D. y=-x2+2x+3或y=x2-2x-3
查看答案和解析>>
科目:初中数学 来源: 题型:
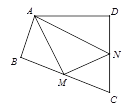
【题目】四边形ABCD中,∠B=∠D=90°,∠C=72°,在BC、CD上分别找一点M、N,使△AMN的周长最小时,∠AMN+∠ANM的度数为_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个动点从点A开始上下来回运动5次,规定向上为正,向下为负。那么这5次运动结果记录如下(单位cm):-5,+7,-3.-11,+3
(1)这个动点停止运动时距离点A多远?在点A的什么位置处?
(2)若这个动点运动速度是2cm/s,运动5次一共需要多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:等腰△ABC的底边BC长为6,面积是18,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )

A. 6 B. 8 C. 9 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了打赢湖北保卫战、武汉保卫战,4万多名医护人员逆行出征,约4万名建设者从八方赶来,并肩奋战,抢建火神山和雷神山医院.他们日夜鏖战,与病毒竞速,创造了10天左右时间建成两座传染病医院的“中国速度”!他们不畏风险,同困难斗争,充分展现团结起来打硬仗的“中国力量”,在建设过程中,有一位木工遇到了这样一道数学题:
有一块矩形木板,木工采用如图的方式,在木板上截出两个面积分别为![]() 和
和![]() 的正方形木板.
的正方形木板.

(1)求剩余木料的面积?
(2)如果木工想从剩余的木料中截出长为![]() ,宽为
,宽为![]() 的长方形木条,最多能截出_________块这样的木条.
的长方形木条,最多能截出_________块这样的木条.
查看答案和解析>>
科目:初中数学 来源: 题型:
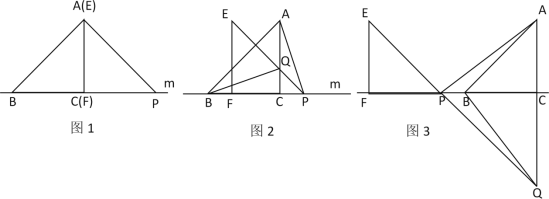
【题目】(1)问题情境,如图1,△ABC的边BC在直线m上,AC⊥BC,且AC=BC,△EFP的边FP也在直线m上,边EF与边AC重合,且EF=FP,
在图1中,AB与AP的数量关系是_______,AB与AP的位置关系是_______
(2)操作发现:将△EFP沿直线m向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ,猜想并证明BQ与AP的数量关系和位置关系
(3)猜想论证:将△EFP沿直线m向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ,(2)中的结论还成立吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com