
【题目】如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,BF交AC于G,连接CF.

(1)求证:△AEF≌△DEB;
(2)若∠BAC=90°,①试判断四边形ADCF的形状,并证明你的结论;
②若AB=8,BD=5,直接写出线段AG的长 .
【答案】(1)详见解析;(2)①四边形ADCF是菱形;详见解析;②2
【解析】
(1)由平行线证明三角形全等所缺少的条件,再根据三角形全等的判定方法证明三角形全等;
(2)①先证四边形ADCF是平行四边形,再证明邻边相等,便可得出结论;
②证明△AFG∽△CBG,得出AG与AC的比例关系,进而由直角三角形的性质求得AC,便可得AG.
(1)∵AF∥BC,
∴∠AFE=∠DBE,
在△AEF和△DEB中,
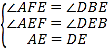 ,
,
∴△AEF≌△DEB(AAS);
(2)①四边形ADCF是菱形,
理由如下:∵△AEF≌△DEB,
∴AF=BD,
∵BD=DC,
∴AF=DC=![]() BC,
BC,
又AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,AD是BC边上的中线,
∴AD=DC,
∴四边形ADCF是菱形;
②∵AF∥BC,
∴△AFG∽△CBG,
∴![]()
∴![]()
∴AG=![]() ,
,
∵BD=5,AD是BC边上的中线,
∴BC=2BD=10,
∵∠BAC=90°,AB=8,
∴AC=![]() ,
,
∴AG=![]() =2,
=2,
故答案为2.


科目:初中数学 来源: 题型:
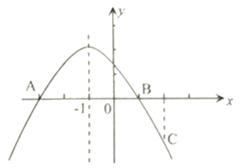
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() 点
点![]() ,点
,点![]() 点
点![]() 是抛物线上任意一点,有下列结论:①
是抛物线上任意一点,有下列结论:①![]() ; ②一元二次方程
; ②一元二次方程![]() 的两个根为
的两个根为![]() 和
和![]() ;③若
;③若![]() ,则
,则![]() ;④对于任意实数
;④对于任意实数![]()
![]() 总成立.其中正确结论的个数为 ( )
总成立.其中正确结论的个数为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,函数
中,函数![]() (
(![]() )的图象G与直线
)的图象G与直线![]() 交于点A(4,1),点B(1,n)(n≥4,n为整数)在直线l上.
交于点A(4,1),点B(1,n)(n≥4,n为整数)在直线l上.
(1)求![]() 的值;
的值;
(2)横、纵坐标都是整数的点叫做整点.记图象![]() 与直线l围成的区域(不含边界)为W.
与直线l围成的区域(不含边界)为W.
①当n=5时,求![]() 的值,并写出区域W内的整点个数;
的值,并写出区域W内的整点个数;
②若区域W内恰有5个整点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一部记录片播放了关于地震的资料及一个有关地震预测的讨论,一位专家指出:“在未来20年,A城市发生地震的机会是三分之二”
对这位专家的陈述下面有四个推断:
①![]() ×20≈13.3,所以今后的13年至14年间,A城市会发生一次地震;
×20≈13.3,所以今后的13年至14年间,A城市会发生一次地震;
②![]() 大于50%,所以未来20年,A城市一定发生地震;
大于50%,所以未来20年,A城市一定发生地震;
③在未来20年,A城市发生地震的可能性大于不发生地震的可能性;
④不能确定在未来20年,A城市是否会发生地震;
其中合理的是( )
A. ①③ B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
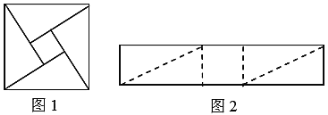
【题目】如图1是三国时期的数学家赵爽创制的一幅“勾股圆方图”.将图2的矩形分割成四个全等三角形和一个正方形,恰好能拼成这样一个“勾股圆方图”,则该矩形与拼成的正方形的周长之比为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
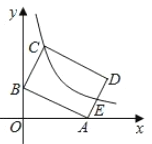
【题目】如图,在平面直角坐标系中,点A(4,0),B(0,2),反比例函数![]() 的图象经过矩形ABCD的顶点C,且交边AD于点E,若E为AD的中点,则k的值为__________.
的图象经过矩形ABCD的顶点C,且交边AD于点E,若E为AD的中点,则k的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
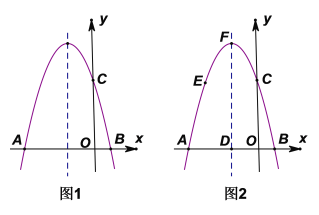
【题目】如图,抛物线![]()
![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,
,![]() 、
、![]() 两点间的距离为
两点间的距离为![]() ,抛物线的对称轴为
,抛物线的对称轴为![]() .
.
(1)求抛物线的解析式;
(2)如图1,对称轴上是否存在点![]() ,使
,使![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)如图2,抛物线的顶点为![]() ,对称轴交
,对称轴交![]() 轴于点
轴于点![]() ,点
,点![]() 为抛物线上一点,点
为抛物线上一点,点![]() 不与点
不与点![]() 重合. 当
重合. 当![]() 时,过点
时,过点![]() 分别作
分别作![]() 轴的垂线和平行线,与
轴的垂线和平行线,与![]() 轴交于点
轴交于点![]() 、与对称轴交于点
、与对称轴交于点![]() ,得到矩形
,得到矩形![]() ,求矩形
,求矩形![]() 周长的最大值;
周长的最大值;
查看答案和解析>>
科目:初中数学 来源: 题型:
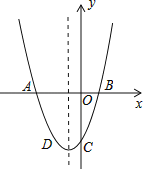
【题目】(2019秋潮阳区校级月考)已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求△PAD周长的最小值;
(3)抛物线的对称轴上有一动点M,当△MAD是等腰三角形时,直接写出M点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com