
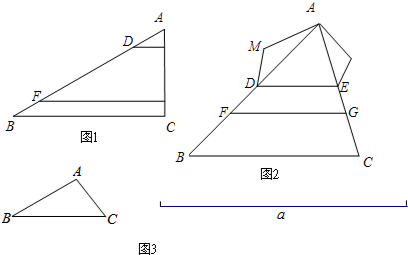
分析 (1)只需利用基本事实“两条直线被一组平行线所截,所得的对应线段成比例”即可解决问题;
(2)要证∠M=∠N,只需证△AMD∽△ANE,只需证$\frac{AD}{AE}$=$\frac{DM}{EN}$=$\frac{AM}{AN}$,由于DF=DM,EG=EN,BF=AM,GC=AN,只需证$\frac{AD}{AE}$=$\frac{DF}{EG}$=$\frac{BF}{GC}$,根据“两条直线被一组平行线所截,所得的对应线段成比例”即可解决问题;
(3)借鉴图2,可进行以下操作:①延长BA到D,使得AD=AC,延长AB到E,使得BE=BC;②过点D画一条线段DF,使得DF=a,连接EF;③过点B作∠DBB′=∠DEF,交DF于点B′,过点A作∠DAA′=∠DEF,交DF于点A′,即可得到AA′∥BB′∥EF;④以点A′为圆心,A′D为半径画弧,以点B′为圆心,B′F为半径画弧,两弧交于点C′;⑤连接A′C′,B′C′,如图4,△A′B′C′即为所求作.
解答 解:(1)如图1,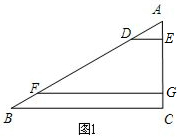
∵DE∥FG∥BC,
∴$\frac{AD}{DF}=\frac{AE}{EG}$,$\frac{DF}{BF}=\frac{EG}{GC}$,
∴$\frac{AD}{AE}$=$\frac{DF}{EG}$=$\frac{BF}{GC}$.
∵AD=2,AE=1,DF=6,
∴$\frac{2}{1}$=$\frac{6}{EG}$=$\frac{BF}{GC}$,
∴EG=3,$\frac{BF}{GC}$=2.
故答案分别为:3、2;
(2)如图2,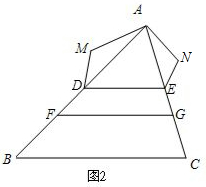
∵DE∥FG∥BC,
∴$\frac{AD}{DF}=\frac{AE}{EG}$,$\frac{DF}{BF}=\frac{EG}{GC}$,
∴$\frac{AD}{AE}$=$\frac{DF}{EG}$=$\frac{BF}{GC}$.
∵DF=DM,EG=EN,BF=AM,GC=AN,
∴$\frac{AD}{AE}$=$\frac{DM}{EN}$=$\frac{AM}{AN}$,
∴△AMD∽△ANE,
∴∠M=∠N;
(3)步骤:
①延长BA到D,使得AD=AC,延长AB到E,使得BE=BC;
②过点D画一条线段DF,使得DF=a,连接EF;
③过点B作∠DBB′=∠DEF,交DF于点B′,过点A作∠DAA′=∠DEF,交DF于点A′;
④以点A′为圆心,A′D为半径画弧,以点B′为圆心,B′F为半径画弧,两弧交于点C′;
⑤连接A′C′,B′C′,如图4,△A′B′C′即为所求作.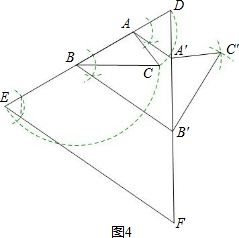
点评 本题从一个基本事实(平行线分线段成比例)出发,经历初步体验、深入探究的过程,在解决问题的过程中,用到了平行线分线段成比例、相似三角形的判定与性质、平行线的判定,考查了操作能力以及运用已有经验解决问题的能力,体现了新课程理念.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,以AB为直径的⊙O交AC于D,已知CD=AD.
如图,△ABC中,以AB为直径的⊙O交AC于D,已知CD=AD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
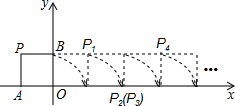 如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2003次,点P依次落在点P1、P2、P3、P4…Pn的位置,则P2003的横坐标x2003=2002.
如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2003次,点P依次落在点P1、P2、P3、P4…Pn的位置,则P2003的横坐标x2003=2002.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=3,∠BAC+∠EAD=180°,求点A到BC的距离.
如图,直径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=3,∠BAC+∠EAD=180°,求点A到BC的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com