
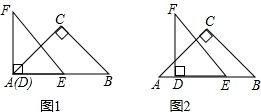
 如图1,△ABC和△DEF都是等腰直角三角形,其中∠C=∠EDF=90°,点A与点D重合,点E在AB上,AB=4,DE=2.如图2,△ABC保持不动,△DEF沿着线段AB从点A向点B移动,当点D与点B重合时停止移动.设AD=x,△DEF与△ABC重叠部分的面积为y,则y关于x的函数图象大致是( )
如图1,△ABC和△DEF都是等腰直角三角形,其中∠C=∠EDF=90°,点A与点D重合,点E在AB上,AB=4,DE=2.如图2,△ABC保持不动,△DEF沿着线段AB从点A向点B移动,当点D与点B重合时停止移动.设AD=x,△DEF与△ABC重叠部分的面积为y,则y关于x的函数图象大致是( )| A. |  | B. | 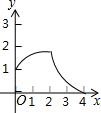 | C. | 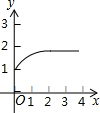 | D. | 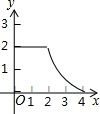 |
分析 要找出准确反映y与x之间对应关系的图象,需分析在不同阶段中y随x变化的情况,由题意知,在△DEF移动的过程中,阴影部分总为等腰直角三角形;据此根据重合部分的斜边长的不同分情况讨论求解.
解答  解:由题意知:在△DEF移动的过程中,阴影部分总为等腰直角三角形.
解:由题意知:在△DEF移动的过程中,阴影部分总为等腰直角三角形.
当0<x≤2时,此时重合部分的斜边长为x,则y=$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$(x+2)×$\frac{\sqrt{2}}{2}$(x+2)-$\frac{1}{2}$x2=-$\frac{1}{4}$x2+x+1.
当2<x≤4时,此时重合部分的斜边长为2,则y=$\frac{1}{2}$(x-4)2;
当4<x≤6时,此时重合部分的斜边长为2-(x-4)=6-x,则y=(6-x)×$\frac{6-x}{2}$×$\frac{1}{2}$=$\frac{1}{4}$x2-3x+9;
由以上分析可知,这个分段函数的图象左边为抛物线的一部分,中间为直线的一部分,右边为抛物线的一部分.
故选:B.
点评 本题以动态的形式考查了分类讨论的思想,函数的知识和等腰直角三角形,具有很强的综合性.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
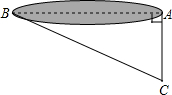 如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上点,测得BC=60m,AC=20m,则A,B两点问的距离40$\sqrt{2}$m.
如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上点,测得BC=60m,AC=20m,则A,B两点问的距离40$\sqrt{2}$m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
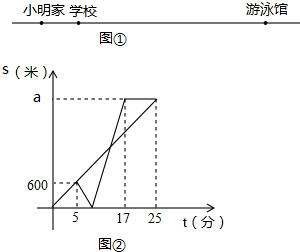 图①是小明家、学校和游泳馆之间的位置关系示意图,某天放学后,小亮和小明同时从学校出发,小亮匀速步行前往游泳馆,小明先匀速步行回家取游泳用品,然后骑自行车原路返回,沿与小亮相同的路线前往游泳馆,小明骑自行车的速度始终不变,小亮和小明各自与学校的距离s(米)与所用时间t(分)之间的函数图象的如图②所示.
图①是小明家、学校和游泳馆之间的位置关系示意图,某天放学后,小亮和小明同时从学校出发,小亮匀速步行前往游泳馆,小明先匀速步行回家取游泳用品,然后骑自行车原路返回,沿与小亮相同的路线前往游泳馆,小明骑自行车的速度始终不变,小亮和小明各自与学校的距离s(米)与所用时间t(分)之间的函数图象的如图②所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
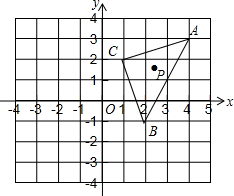 在平面直角坐标系中,△ABC的三个顶点的位置如图,P为△ABC内一点,P的坐标为(a,b).
在平面直角坐标系中,△ABC的三个顶点的位置如图,P为△ABC内一点,P的坐标为(a,b).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
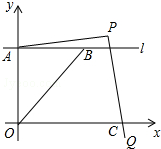 如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.
如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
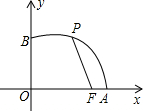 如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}$x(0≤x≤5),则结论:①AF=2;②BF=4;③OA=5;④OB=3,正确结论的序号是( )
如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}$x(0≤x≤5),则结论:①AF=2;②BF=4;③OA=5;④OB=3,正确结论的序号是( )| A. | ①②③ | B. | ①③ | C. | ①②④ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①④ | B. | ③④ | C. | ②③ | D. | ④⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com