
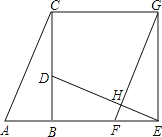
【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线AB平移至△FEG,DE、FG相交于点H.
(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
【答案】(1)FG⊥ED.理由见解析;(2)证明见解析.
【解析】试题分析: (1)根据旋转和平移可得∠DEB=∠ACB,∠GFE=∠A,再根据∠ABC=90°可得∠A+∠ACB=90°,进而得到∠DEB+∠GFE=90°,从而得到DE、FG的位置关系是垂直;(2)根据旋转和平移找出对应线段和角,然后再证明是矩形,后根据邻边相等可得四边形CBEG是正方形.
试题解析:
(1)解:FG⊥ED.理由如下:
∵△ABC绕点B顺时针旋转90°至△DBE后,∴∠DEB=∠ACB,
∵把△ABC沿射线平移至△FEG,∴∠GFE=∠A,∵∠ABC=90°,
∴∠A+∠ACB=90°,∴∠DEB+∠GFE=90°,∴∠FHE=90°,∴FG⊥ED;
(2)证明:根据旋转和平移可得∠GEF=90°,∠CBE=90°,CG∥EB,CB=BE,
∵CG∥EB,∴∠BCG=∠CBE=90°,∴四边形BCGE是矩形,∵CB=BE,
∴四边形CBEG是正方形.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
【题目】给出下列命题:
(1)平行四边形的对角线互相平分;(2)矩形的对角线相等;(3)菱形的对角线互相垂直平分;(4)正方形的对角线相等且互相垂直平分.其中,真命题的个数是( )
A. 2B. 3C. 4D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
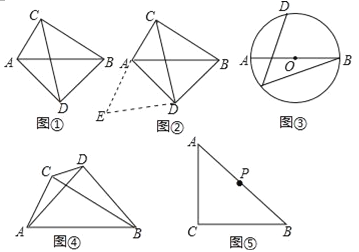
如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC,BC,CD之间的数量关系.
小吴同学探究此问题的思路是:将△BCD绕点D,逆时针旋转90°到△AED处,点B,C分别落在点A,E处(如图②),易证点C,A,E在同一条直线上,并且△CDE是等腰直角三角形,所以CE=![]() CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC=![]() CD.
CD.
简单应用:
(1)在图①中,若AC=![]() ,BC=
,BC=![]() ,则CD= .
,则CD= .
(2)如图③,AB是⊙O的直径,点C、D在⊙上,![]() ,若AB=13,BC=12,求CD的长.
,若AB=13,BC=12,求CD的长.
拓展规律:
(3)如图④,∠ACB=∠ADB=90°,AD=BD,若AC=m,BC=n(m<n),求CD的长(用含m,n的代数式表示)
(4)如图⑤,∠ACB=90°,AC=BC,点P为AB的中点,若点E满足AE=![]() AC,CE=CA,点Q为AE的中点,则线段PQ与AC的数量关系是 .
AC,CE=CA,点Q为AE的中点,则线段PQ与AC的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要了解某市九年级学生的视力状况,从中抽查了500名学生的视力状况,那么样本是指( )
A. 某市所有的九年级学生
B. 被抽查的500名九年级学生
C. 某市所有的九年级学生的视力状况
D. 被抽查的500名学生的视力状况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市教育行政部门为了了解七年级学生每学期参加综合实践活动的情况,随机抽样调查了某校七学生一个学期参加综合实践活动的天数,并用得到的数据绘制了如图两幅不完整的统计图.
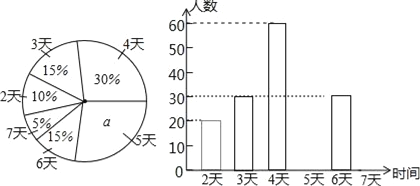
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中的a的值,并求出该校七年级学生总数;
(2)分别求出活动时问为5天、7天的学生人数,并补全频数分布直方图;
(3)求出扇形统计图中“活动时间为4天”的扇形所对圆心角的度数;
(4)如果该市共有七年级学生6000人,请你估计“活动时间不小于4天”的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的2016年6月份的日历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )

A. 27 B. 51 C. 69 D. 72
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com