
��ͼ��ijУһ����ѧ��¥�Ķ�������һ�顰�����������������桱��������CD��С����ɽ�µ��½�A����������Ƶײ�D������Ϊ60�㣬��ɽ�������ߵ�B����������ƶ���C������Ϊ45�㣮��֪ɽ��AB���¶�i=1��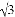 ��AB=10�ף�AE=15�ף������������CD�ĸ߶ȣ���������ĸ߶Ⱥ��Բ��ƣ������ȷ��0.1�ף��ο����ݣ�
��AB=10�ף�AE=15�ף������������CD�ĸ߶ȣ���������ĸ߶Ⱥ��Բ��ƣ������ȷ��0.1�ף��ο����ݣ�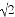 ��1.414��
��1.414��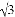 ��1.732����
��1.732����


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�����Ϻӿ���2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��һ�������IJ�����װ��������ŷֱ�Ϊ1��2��3��С�����ǵIJ��ʡ���״����С��ȫ��ͬ��С���Ӳ��������ȡ��һ��С��������Ϊx��Ȼ��С��Żز�����С���ٴӲ��������ȡ��һ��С��������Ϊy������ȷ���˵�A������Ϊ��x��y���������б�������ͼ�ķ��������A�ں��� ͼ���ϵĸ��ʣ�
ͼ���ϵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�걱ʦ������꼶��ѧ�ϲ��5�� һԪһ�η��� ��Ԫ���Ծ� ���ͣ���ѡ��
��֪x����3�Ƿ���k(x��4)��2k��x��5�Ľ⣬��k��ֵ��(����)
A. ��2 B. 2 C. 3 D. 5
A �������������������x=-3����k��x+4��-2k-x=5�� �ã�k����-3+4��-2k+3=5�� ��ã�k=-2�� ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������Т����2016-2017ѧ����꼶���ϣ���ĩ������ѧ�Ծ� ���ͣ���ѡ��
��ͼ��BD��CE�ֱ��ǡ�ABC�����ߣ�BD��CE���ڵ�O�������н�������ȷ���ǣ�������

A.  B.
B. 
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�������ʡ�����жŶ������ؾ��꼶���ϣ���ĩ��ѧ�Ծ�������ѧ�ƣ� ���ͣ������
��֪����ͼ��������y=��x2+bx+c����ֱ��y=��x+3�����������������A��B������������x�����һ������ΪC�������ߵĶ���ΪD��
��1����������ߵĽ���ʽ��
��2������MΪ��������һ���㣬�Ƿ���ڵ�M��ʹ��ACM���ABC�������ȣ������ڣ����M�����ꣻ�������ڣ���˵�����ɣ�
��3����x�����Ƿ���ڵ�Nʹ��ADNΪֱ�������Σ������ڣ�ȷ����N�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�������ʡ�����жŶ������ؾ��꼶���ϣ���ĩ��ѧ�Ծ�������ѧ�ƣ� ���ͣ������
��ͼ���ı���ABCD�ڽ��ڡ�O��EΪCD�ӳ�����һ�㣮����B=110�㣬���ADE�Ķ���Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�������ʡ�����жŶ������ؾ��꼶���ϣ���ĩ��ѧ�Ծ�������ѧ�ƣ� ���ͣ���ѡ��
���κ���y��ax2��bx��c��a��0���Ĵ���ͼ����ͼ��ʾ��1��x��h��2��0��xA��1�������н��ۣ��� 2a��b��0���� abc��0���� ��OC��2OA����2b��ac = 4���� 3a��c��0��������ȷ�ĸ����ǣ� ��

A. 1 B. 2 C. 3 D. 4
C ������������������١������ߵĿ������£� ��a��0�� �������ߵĶԳ���-��1�� ��b��-2a����2a+b��0���ٳ����� �ڡ�b��-2a��a��0�� ��b��0�� ����������y��Ľ�����y��ĸ����ᣬ ��c��0�� ��abc��0���ڴ��� �۵�A�ĺ�����Ϊ����C��������Ϊc�� ��OC=2OA�� ��-c=�������ã�2b-ac=4����...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ��ʦ����ϲ��4�� ����ƽ��ͼ�� ��Ԫ���Ծ� ���ͣ������
��ͼ���ڡ�AOB�У�OD�ǡ�BOC��ƽ���ߣ�OE�ǡ�AOC��ƽ���ߣ�����AOB��135�㣬���EOD��____��
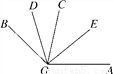
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ��ͷ�гκ���2018����꼶��ѧ����ĩ���������ѧ�Ծ� ���ͣ������
��ͼ����O�ǡ�ABC�����Բ����ABC=45�㣬AD�ǡ�O�����߽�BC���ӳ�����D��AB��OC��E��

��1����֤��AD��OC��
��2����AE=2 ��CE=2�����O�İ뾶���߶�BE�ij���
��CE=2�����O�İ뾶���߶�BE�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com