
【题目】如图,∠AOB=90°,∠BOC=30°,射线OM平分∠AOC,ON平分∠BOC. 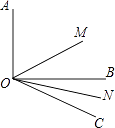
(1)求∠MON的度数;
(2)如果(1)中,∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中,∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)、(2)、(3)的结果中,你能看出什么规律?
【答案】
(1)解:∠AOB=90°,∠BOC=30°,
∴∠AOC=90°+30=120°.
由角平分线的性质可知:∠MOC= ![]() ∠AOC=60°,∠CON=
∠AOC=60°,∠CON= ![]() ∠BOC=15°.
∠BOC=15°.
∵∠MON=∠MOC﹣∠CON,
∴∠MON=60°﹣15°=45°
(2)解:∠AOB=α,∠BOC=30°,
∴∠AOC=α+30°.
由角平分线的性质可知:∠MOC= ![]() ∠AOC=
∠AOC= ![]() α+15°,∠CON=
α+15°,∠CON= ![]() ∠BOC=15°.
∠BOC=15°.
∵∠MON=∠MOC﹣∠CON,
∴∠MON= ![]() α+15°﹣15°=
α+15°﹣15°= ![]() α
α
(3)解:∠AOB=90°,∠BOC=β,
∴∠AOC=β+90°.
由角平分线的性质可知:∠MOC= ![]() ∠AOC=
∠AOC= ![]() β+45°,∠CON=
β+45°,∠CON= ![]() ∠BOC=
∠BOC= ![]() β.
β.
∵∠MON=∠MOC﹣∠CON,
∴∠MON= ![]() β+45°﹣
β+45°﹣ ![]() β=45°
β=45°
(4)解:根据(1)、(2)、(3)可知∠MON= ![]() ∠BOA,与∠BOC的大小无关
∠BOA,与∠BOC的大小无关
【解析】(1)先求得∠AOC的度数,然后由角平分线的定义可知∠MOC=60°,∠CON=15°,最后根据∠MON=∠MOC﹣∠CON求解即可;(2)先求得∠AOC=α+30°,由角平分线的定义可知∠MOC= ![]() α+15°,∠CON=15°,最后根据∠MON=∠MOC﹣∠CON求解即可;(3)先求得∠AOC=β+90°,由角平分线的定义可知∠MOC=
α+15°,∠CON=15°,最后根据∠MON=∠MOC﹣∠CON求解即可;(3)先求得∠AOC=β+90°,由角平分线的定义可知∠MOC= ![]() β+15°,∠CON=
β+15°,∠CON= ![]() β,最后根据∠MON=∠MOC﹣∠CON求解即可;(4)根据计算结果找出其中的规律即可.
β,最后根据∠MON=∠MOC﹣∠CON求解即可;(4)根据计算结果找出其中的规律即可.


科目:初中数学 来源: 题型:
【题目】毕达哥拉斯学派对“数”与“形”的巧妙结合作了如下研究: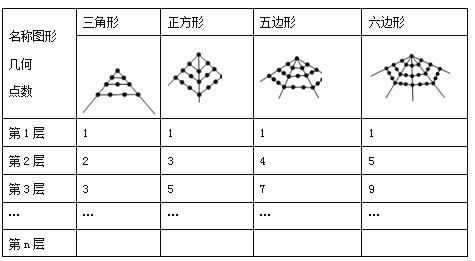
(1)六边形第5层的几何点数是 ;第n层的几何点数是 .
(2)在第 层时,六边形的几何点数是三角形的几何点数的3.5倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市2017年实现生产总值达280亿的目标,用科学记数法表示“280亿”为( )
A. 28×109 B. 2.8×108 C. 2.8×109 D. 2.8×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】林城市对教师试卷讲评课中学生参与的深度与广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如下两幅不完整的统计图,请根据图中所给信息解答下列问题:
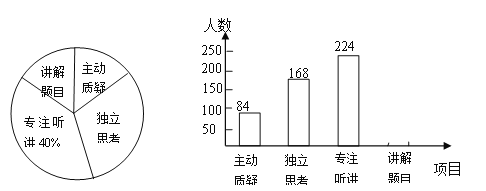
(1)在这次评价中,一共抽查了 名学生;
(2)请将条形图补充完整;
(3)如果全市有16万名初中学生,那么在试卷评讲课中,“独立思考”的学生约有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农大毕业的小王回乡自主创业,在大棚中栽培新品种的蘑菇,该种蘑菇在18℃的条件下生长最快,因此用装有恒温系统的大棚栽培,每天只开启一次,如图是某天恒温系统从开启升温到保持恒温及关闭.大棚内温度y(℃)随时间x(时)变化的函数图象,其中BC段是函数y=![]() (k>0)图象的一部分.若该蘑菇适宜生长的温度不低于12℃,则这天该种蘑菇适宜生长的时间为( )
(k>0)图象的一部分.若该蘑菇适宜生长的温度不低于12℃,则这天该种蘑菇适宜生长的时间为( )
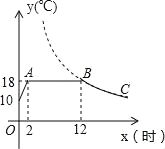
A.18小时 B.17.5小时 C.12小时 D.10小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4cm, AD=2![]() cm,E为CD边上的中点,点P从点A沿折线AE﹣EC运动到点C时停止,点Q从点A沿折线AB﹣BC运动到点C时停止,它们运动的速度都是1cm/s.如果点P,Q同时开始运动,设运动时间为t(s),△APQ的面积为y(cm2),则y与t的函数关系的图象可能是( )
cm,E为CD边上的中点,点P从点A沿折线AE﹣EC运动到点C时停止,点Q从点A沿折线AB﹣BC运动到点C时停止,它们运动的速度都是1cm/s.如果点P,Q同时开始运动,设运动时间为t(s),△APQ的面积为y(cm2),则y与t的函数关系的图象可能是( )
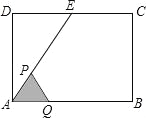
A.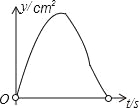
B.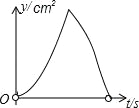
C.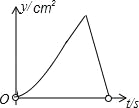
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,电子蚂蚁P从点A分别以1个单位/秒的速度顺时针绕正方形运动,电子蚂蚁Q从点A以3个单位/秒的速度逆时针绕正方形运动,则第2017次相遇在( ) 
A.点 A
B.点B
C.点C
D.点D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对数(生于公元250年左右)是中国数字史上伟大的数学家,在世界数学史上,也占着重要的地位,他的杰作《九章算术法》和《海岛算经》是我国宝贵的数学遗产.
(1)其中一卷书研究的对象全是有关高与距离的测量,所使用的工具也都是利用垂直关系所连接起来的测杆与横棒,所有问题都是利用两次或多次测量所得的数据,来推算可望而不可及的目标的高、深、广、远,此书收集于明成祖时编修的永乐大典中,现保存在英国剑桥大学图书馆,该卷书是 海岛算经 ;
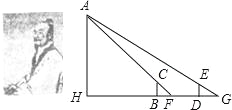
(2)在(1)中提到刘嶶的杰作中,记载的第一个问题的大意是:在如图所示的示意图中,要测量海岛上一座山峰的高度AH,立两根高3丈的标杆BC和DE,两杆之间的距离BD=1000步,点D、B、H成一线,从B处退行123步到点F处,人的眼睛贴着地面观察点A,点A、C、F也成一线,从D处退行127步到点G处,人的眼睛贴着地面观察点A,点A,E,G也成一线,求AH有多少丈,HB有多少步(这里1步=6尺,1丈=10尺)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com