
【题目】若经过一个三角形某一顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形过该顶点的生成三角形.

(1)如图,在等腰Rt△ABC中,AB=AC,∠A=90°,请问△ABC是否是生成三角形?请你说明理由.
(2)若△ABC是等腰三角形过顶点B的生成三角形,∠C是其最小的内角,请探求∠ABC与∠C之间的关系.
【答案】(1)△ABC是生成三角形,理由见解析;(2)∠ABC=3∠C,理由见解析.
【解析】
(1)作等腰三角形底边上的高是常用的辅助线作法,可把等腰直角三角形分成等腰直角三角形;
(2)根据等腰三角形的性质和外角的性质即可得到结论.
(1)证明:过点A作AD⊥BC,垂足为D.
∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°,∠BAD=∠CAD=![]() ∠BAC=45°,
∠BAC=45°,
∴∠B=∠BAD,∠C=∠CAD.
∴△ABD和△ACD是等腰三角形,
∴△ABC是生成三角形
(2)如图1所示,在△ABC中,∵AC=BC,
∴∠CAB=∠CBA,
当BD=CD=AB,
∴∠C=∠CBD,∠A=∠ADB,
∵∠ADB=∠C+∠CBD=2∠C=∠A,
∴∠ABC=2∠C,
当BD=CD,AB=AD时,∠ABC=3∠C.
如图2,由题意得:AB=BC=AD,BD=CD,
∴∠C=∠A=∠CBD,∠ABD=∠ADB,
∵∠ADB=∠C+∠CBD=2∠C,
∴∠ABD=2∠C,
∴∠ABC=3∠C.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】这是一道我们曾经探究过的问题:如图1.等腰直角三角形![]() 中,
中,![]() ,
,![]() .直线
.直线![]() 经过点
经过点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() .易证得
.易证得![]() ≌
≌![]() .(无需证明),我们将这个模型称为“一线三等角”或者叫“K形图”.接下来,我们就利用这个模型来解决一些问题:
.(无需证明),我们将这个模型称为“一线三等角”或者叫“K形图”.接下来,我们就利用这个模型来解决一些问题:
(模型应用)
(1)如图2.已知直线l1:![]() 与与坐标轴交于点A、B.以AB为直角边作等腰直角三角形ABC,若存在,请求出C的坐标;不存在,若说明理由.
与与坐标轴交于点A、B.以AB为直角边作等腰直角三角形ABC,若存在,请求出C的坐标;不存在,若说明理由.

(2)如图3已知直线l1:![]() 与坐标轴交于点A、B.将直线l1绕点A逆时针旋转45°至直线l2.直线l2在x轴上方的图像上是否存在一点Q,使得△QAB是以QA为底的等腰直角三角形?若存在,请求出直线BQ的函数关系式;若不存在,说明理由.
与坐标轴交于点A、B.将直线l1绕点A逆时针旋转45°至直线l2.直线l2在x轴上方的图像上是否存在一点Q,使得△QAB是以QA为底的等腰直角三角形?若存在,请求出直线BQ的函数关系式;若不存在,说明理由.
(拓展延伸)
(3)直线AB:![]() 与
与![]() 轴负半轴、
轴负半轴、![]() 轴正半轴分别交于A、B两点.分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE,连EF交y轴于P点,如图4,△EPB的面积是否确定?若确定,请求出具体的值;若不确定,请说明理由.
轴正半轴分别交于A、B两点.分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE,连EF交y轴于P点,如图4,△EPB的面积是否确定?若确定,请求出具体的值;若不确定,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图象交
的图象交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在射线
在射线![]() 上,且
上,且![]() .
.![]() 垂直
垂直![]() 轴于点
轴于点![]() .
.
![]() 点
点![]() 坐标为________,点
坐标为________,点![]() 坐标为________.
坐标为________.
![]() 操作:将一足够大的三角板的直角顶点
操作:将一足够大的三角板的直角顶点![]() 放在射线
放在射线![]() 或射线
或射线![]() 上,一直角边始终过点
上,一直角边始终过点![]() ,另一直角边与
,另一直角边与![]() 轴相交于点
轴相交于点![]() .问是否存在这样的点
.问是否存在这样的点![]() ,使以点
,使以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?若存在,求出点
全等?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
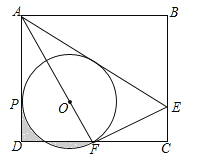
【题目】(2017四川省达州市,第16题,3分)如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P.若AB=6,BC=![]() ,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=
,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=![]() CE;④
CE;④![]() .其中正确结论的序号是__________.
.其中正确结论的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ABC,∠ACB的平分线交于点O,D是外角与内角平分线交点,E是外角平分线交点,若∠BOC=120°,则∠D=_____;∠E=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 是
是![]() 延长线上一点,点
延长线上一点,点![]() 是线段
是线段![]() 上一点,
上一点,![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() 是等边三角形;④
是等边三角形;④![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )

A.1B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:通过小学的学习我们知道,分数可分为“真分数”和“假分数”,而假分数都可化为带分数,如:![]() 我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.
我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.
如![]() 这样的分式就是假分式;再如:
这样的分式就是假分式;再如:![]() ,
,![]() 这样的分式就是真分式
这样的分式就是真分式![]() 类似的,假分式也可以化为带分式(即:整式与真分式的和的形式)
类似的,假分式也可以化为带分式(即:整式与真分式的和的形式)
如:![]() ;
;
解决下列问题:
(1)分式![]() 是______分式(填“真分式”或“假分式”);
是______分式(填“真分式”或“假分式”);
(2)将假分式![]() 化为带分式;
化为带分式;
(3)如果x为整数,分式![]() 的值为整数,求所有符合条件的x的值.
的值为整数,求所有符合条件的x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2k-1)x+k2=0有两个实根x1和x2
(1) 求实数k的取值范围
(2) 若方程两实根x1、x2满足x12-x22=0,求k的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=﹣![]() ,y=
,y=![]() 的图象交于B、A两点,则tan∠OAB的值的变化趋势为( )
的图象交于B、A两点,则tan∠OAB的值的变化趋势为( )
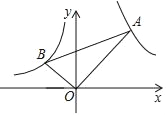
A. 逐渐变小 B. 逐渐变大 C. 时大时小 D. 保持不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com