
【题目】如图,AB是⊙O的直径,经过圆上点D的直线CD恰∠ADC=∠B。

(1)求证:直线CD是⊙O的的切线;
(2)过点A作直线AB的垂线交BD的延长线于点E,且AB=![]() ,BD=2,求线段AE的长。
,BD=2,求线段AE的长。
【答案】解:(1)证明:连接OD,
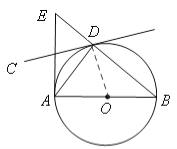
∵OB=OD,∴∠ODB=∠B。
又∵∠ADC=∠B,∴∠ODB=∠ADC。
∵AB是⊙O的直径,∴∠ADB=900。
∴∠ODC=∠ADC +∠ADO= ∠ODB+∠ADO= ∠ADB=900。
又 ∵OD是⊙O的半径,∴直线CD是⊙O的的切线。
BC=OC﹣OB=30﹣20=10(千米)。
(2)在Rt△ABD中,∵AB=![]() ,BD=2,∴根据勾股定理得AD=1。
,BD=2,∴根据勾股定理得AD=1。
∵AE⊥AB,∴∠EAB=900。∴∠EAB=∠ADB =900。
又∵∠B=∠B,∴△ABD∽△EBA。∴![]() ,即
,即![]() 。∴
。∴![]() 。
。
【解析】(1)连接OD,只要证明∠ODC=∠ADC +∠ADO= ∠ODB+∠ADO= ∠ADB=900即可。
(2)根据勾股定理求得AD=1,则由△ABD∽△EBA可列比例式求解。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的实验时,绘出的某一结果出现的频率折线图,则符合这一结果的实验可能是( )

A. 抛一枚硬币,出现正面朝上
B. 掷一个正六面体的骰子,出现3点朝上
C. 一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D. 从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…,第n次移动到An.则△OA2A2018的面积是( )
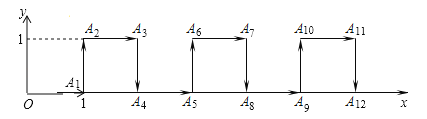
A. 504m2 B. ![]() m2 C.
m2 C. ![]() m2 D. 1009m2
m2 D. 1009m2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.
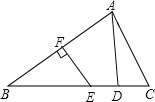
(1)求证:AD⊥BC.
(2)若∠BAC=75°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE.对于下列结论:①AD=DC;②△CBA∽△CDE;③![]() =
=![]() ;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )
;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )

A. ①② B. ①②③ C. ①④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成作图:

(1)作出△ABC关于x轴对称的图形;
(2)写出A、B、C的对应点A′、B′、C′的坐标;
(3)在x轴上画出点Q,使△QAC的周长最小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△AOD是等腰直角三角形,AB=AC,AO=AD,∠BAC=∠OAD=90°,点O是△ABC内的一点,∠BOC=130°.
(1)由已知条件可知哪两个三角形全等__________,理由_________.
(2)求∠DCO的大小.
(3)设∠AOB=α,那么当α为多少度时,△COD是等腰三角形.
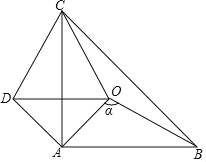
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com