Question

【题目】如图，直线y=mx+n交坐标轴分别于A，B（0，1）两点，交双曲线y=于点C（2，2），点D在直线AB上，AC=2CD．过点D作DE⊥x轴于点E，交双曲线y=于点F，连接CF．

（1）求反比例函数y=和直线y=mx+n的表达式；

（2）求△CDF的面积．

Answer 1

【答案】（1）y=x+1；y= （2）2

【解析】

（1）根据待定系数法即可求得；

（2）作CH⊥x轴于H，根据平行线的性质求得DE，进一步求得D的坐标，把D的横坐标代入反比例函数y=中，求得F点的坐标，从而求得DF，然后根据三角形面积公式即可求得．

（1）∵直线y=mx+n经过B（0，1），C（2，2）两点，∴，解得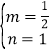：，∴直线的表达式为y=；

∵点C（2，2）在双曲线y=上，∴2=，解得：k=4，∴反比例函数的解析式为y=；

（2）作CH⊥x轴于H．

∵C（2，2），∴CH=2．

∵DE⊥x轴于点E，∴CH∥DE，∴==．

由直线y=x+1可知A（﹣2，0），∴OA=2，AH=4．

∵AC=2CD，∴===，∴DE=3，AE=6，∴D（4，3）．

把x=4代入y=得：y=1，∴F（4，1），∴DF=3﹣1=2，∴△CDF的面积=×2×（4﹣2）=2．