
【题目】已知:如图,在Rt△ABC中,∠C=90°,Rt△ABC的内切圆⊙O,切点分别为点D、E、F,
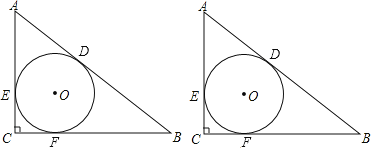
(1)若AC=3,BC=4,求△ABC的内切圆半径;
(2)当AD=5,BD=7时,求△ABC的面积;
(3)当AD=m,BD=n时,直接写出求△ABC的面积(用含m,n的式子表示)为 .
【答案】(1)1;(2)35;(3)mn
【解析】
(1)连接OD、OE、OF,如图,设⊙O的半径为r,利用勾股定理计算出AB=5,利用切线的性质和切线长定理得到OE⊥AC,OF⊥BC,CE=CF,AE=AD,BF=BD,则四边形CFOE为正方形,所以CE=CF=OE=r,从而得3﹣r+4﹣r=5,然后求出r即可;
(2)设⊙O的半径为r,利用(1)中的结论得到AE=AD=5,BF=BD=7,AC=5+r,BC=7+r,再利用勾股定理得到(5+r)2+(7+r)2=(5+7)2,求出r得到AC=![]() ﹣1,BC=
﹣1,BC=![]() +1,然后根据三角形面积公式求解;
+1,然后根据三角形面积公式求解;
(3)设⊙O的半径为r,与(2)一样得到AE=AD=m,BF=BD=n,AC=m+r,BC=n+r,利用勾股定理得到(m+r)2+(n+r)2=(m+n)2,解得r=![]() 或r=
或r=![]() (舍去),所以AC=
(舍去),所以AC=![]() ),BC=
),BC=![]() ,然后利用勾股定理计算三角形的面积即可.
,然后利用勾股定理计算三角形的面积即可.
解:(1)连接OD、OE、OF,如图,设⊙O的半径为r,
在Rt△ABC中,AB=![]() =5,
=5,
∵Rt△ABC的内切圆⊙O,切点分别为点D、E、F,
∴OE⊥AC,OF⊥BC,CE=CF,AE=AD,BF=BD,
易得四边形CFOE为正方形,
∴CE=CF=OE=r,
∴AD=AE=3﹣r,BD=BF=4﹣r,
∴3﹣r+4﹣r=5,解得r=1,
即△ABC的内切圆半径为1;
(2)设⊙O的半径为r,
由(1)得AE=AD=5,BF=BD=7,
∴AC=5+r,BC=7+r,
在Rt△ABC中,(5+r)2+(7+r)2=(5+7)2,解得r=![]() ﹣6或r=
﹣6或r=![]() ﹣6(舍去),
﹣6(舍去),
∴AC=![]() ﹣6+5=
﹣6+5=![]() ﹣1,BC=
﹣1,BC=![]() ﹣6+7=
﹣6+7=![]() +1,
+1,
∴S△ABC=![]() (
(![]() ﹣1)(
﹣1)(![]() +1)=35;
+1)=35;
(3)设⊙O的半径为r,
由(1)得AE=AD=m,BF=BD=n,
∴AC=m+r,BC=n+r,
在Rt△ABC中,(m+r)2+(n+r)2=(m+n)2,解得r=![]() 或r=
或r=![]() (舍去),
(舍去),
∴AC=![]() ,BC=
,BC=![]() ,
,
∴S△ABC=![]() ×AC×BC=
×AC×BC=![]() =
=![]() .
.
故答案为mn.



 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】《孙子算经》是唐初作为“算学”教科书的著名的《算经十书》之一,共三卷,上卷叙述算筹记数的制度和乘除法则,中卷举例说明筹算分数法和开平方法,都是了解中国古代筹算的重要资料,下卷收集了一些算术难题,“鸡兔同笼”便是其中一题.下卷中还有一题,记载为:“今有甲乙二人,持钱各不知数.甲得乙中半,可满四十八;乙得甲太半,亦满四十八.问甲、乙二人持钱各几何?”意思是:“甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱48文.如果乙得到甲所有钱的![]() ,那么乙也共有钱48文.问甲、乙二人原来各有多少钱?”设甲原有钱x文,乙原有钱y文,可得方程组( )
,那么乙也共有钱48文.问甲、乙二人原来各有多少钱?”设甲原有钱x文,乙原有钱y文,可得方程组( )
A.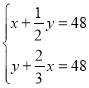 B.
B.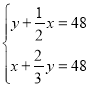 C.
C.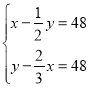 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
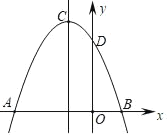
【题目】如图,抛物线y=ax2+bx+c交x轴分别于点A(﹣3,0),B(1,0),交y轴正半轴于点D,抛物线顶点为C.下列结论
①2a﹣b=0;
②a+b+c=0;
③当m≠﹣1时,a﹣b>am2+bm;
④当△ABC是等腰直角三角形时,a=![]() ;
;
⑤若D(0,3),则抛物线的对称轴直线x=﹣1上的动点P与B、D两点围成的△PBD周长最小值为3![]() ,其中,正确的个数为( )
,其中,正确的个数为( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ABC=90°,

(1)如图1,分别过A,C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM~△BCN;
(2)如图2,P是边BC上一点,∠BAP=∠C,PM⊥PA交AC于点M,![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,AD:BC:AC=2:3:5,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程 (m-1)x![]() -mx+1=0。
-mx+1=0。
(1)证明:不论m为何值时,方程总有实数根;
(2)若m为整数,当m为何值时,方程有两个不相等的整数根。
查看答案和解析>>
科目:初中数学 来源: 题型:
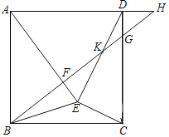
【题目】如图,在边长为4正方形ABCD中,以AB为腰向正方形内部作等腰△ABE,点G在CD上,且CG=3DG.连接BG并延长,与AE交于点F,与AD延长线交于点H.连接DE交BH于点K.若AE2=BFBH,则S△CDE=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AD⊥BC,OE⊥BC,若∠BAC=45°.
(1)求证:OE=![]() BC;
BC;
(2)将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H,若BD=6,CD=4,求AD的长;
(3)作OM⊥AB于M,ON⊥AC于N,在(2)的条件下求![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进货价为30元的台灯以40元的价格售出,平均每月能售出600个,经调查表明,这种台灯的售价每上涨1元,其销量就减少10个,市场规定此台灯售价不得超过60元,为了实现销售这种台灯平均每月10000元的销售利润,售价应定为多少元?这时售出台灯多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
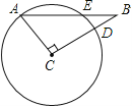
【题目】△ABC中,∠C=Rt∠,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB、BC分别交于点E、D,则AE的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com