
【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D。

(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长。
【答案】(1)证明过程见解析;(2)AC=6.
【解析】
试题分析:(1)连接OD,根据OA=OD得出∠OAD=∠ODA,根据角平分线可得∠OAD=∠DAC,从而可以得出:∠ODA=∠DAC,说明OD∥AC,得到所求的结论;(2)、过点D作DE⊥AB,根据角平分线的性质得到DE=DC=3,AC=AE,根据勾股定理得到BE=4,然后设AC=x,则AB=x+4,BC=8,根据直角△ABC的勾股定理求出AC的长度.
试题解析:(1)、连接OD. ∵ OA=OD AD平分∠BAC ∴ ∠ODA=∠OAD ∠OAD=∠CAD
∴∠ODA=∠CAD ∴ OD//AC ∴ ∠ODB=∠C=90° ∴ BC是⊙O的切线.
(2)过D点作AB的垂线段DE ∴DE=DC=3,BD=5, 则BE=4,
又∵AE=AC,在直角△ABC中运用勾股定理,设AC=x,则![]() 解得:x=6,∴ AC=6
解得:x=6,∴ AC=6


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
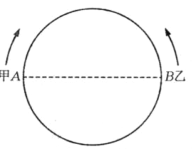
【题目】某校为培养青少年科技创新能力,举办了动漫制作活动,小明设计了点做圆周运动的一个雏型.如图所示,甲、乙两点分别从直径的两端点 A、B以顺时针、逆时针的方向同时沿圆周运动. 甲运动的路程l(cm)与时间t(s)满足关系:![]() (t≥0),乙以4 cm/s的速度匀速运动,半圆的长度为 21 cm.
(t≥0),乙以4 cm/s的速度匀速运动,半圆的长度为 21 cm.
(1)甲运动 4 s后的路程是多少?
(2)甲、乙从开始运动到第一次相遇时,它们运动了多少时间?
(3)甲、乙从开始运动到第二次相遇时,它们运动了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1m,小明爸爸与家之间的距离为s2m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.

(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)交x轴于A(﹣1,0),B(5,0)两点,与y轴交于点C(0,2)
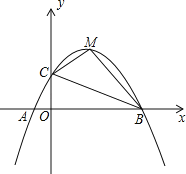
(1)求抛物线的解析式;
(2)若点M为抛物线的顶点,连接BC、CM、BM,求△BCM的面积;
(3)连接AC,在x轴上是否存在点P使△ACP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
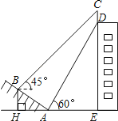
【题目】如图,某大楼的顶部树有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度![]() ,AB=10米,AE=15米.
,AB=10米,AE=15米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
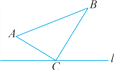
【题目】如图,在△ABC中,∠ACB=90°,AC=6,BC=8.点P从点A出发沿路径A→C→B向终点B运动;点Q从点B出发沿路径B→C→A向终点A运动.点P和点Q分别以1个单位/秒和3个单位/秒的速度同时开始运动,两点都要到相应的终点时才能停止运动,在某一时刻,过点P作PE⊥l于点E,过点Q作QF⊥l于点F.问:点P运动多少时间时,△PEC与△CFQ全等?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com