
ЁОЬтФПЁПвбжЊaЪЧзюДѓЕФИКећЪ§ЃЌbЪЧ-5ЕФЯрЗДЪ§ЃЌc=-|-2|ЃЌЧвaЁЂbЁЂcЗжБ№ЪЧЕуAЁЂBЁЂCдкЪ§жсЩЯЖдгІЕФЪ§ЃЎ
![]()
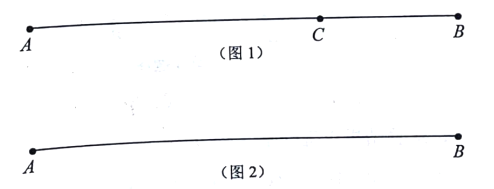
ЃЈ1ЃЉЧѓaЁЂbЁЂcЕФжЕЃЌВЂдкЪ§жсЩЯБъГіЕуAЁЂBЁЂCЃЎ
ЃЈ2ЃЉШєЖЏЕуPДгЕуAГіЗЂбиЪ§жсе§ЗНЯђдЫЖЏЃЌЖЏЕуQЭЌЪБДгЕуBГіЗЂвВбиЪ§жсе§ЗНЯђдЫЖЏЃЌЕуPЕФЫйЖШЪЧУПУы3ИіЕЅЮЛГЄЖШЃЌЕуQЕФЫйЖШЪЧУПУы1ИіЕЅЮЛГЄЖШЃЌЧѓдЫЖЏМИУыКѓЃЌЕуPПЩвдзЗЩЯЕуQЃП
ЃЈ3ЃЉдкЪ§жсЩЯеввЛЕуMЃЌЪЙЕуMЕНAЁЂBЁЂCШ§ЕуЕФОрРыжЎКЭЕШгк12ЃЌЧыЧѓГіЫљгаЕуMЖдгІЕФЪ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉa=-1ЃЌb=5ЃЌc=-2ЃЌЪ§жсМћНтЮіЃЛЃЈ2ЃЉдЫЖЏ3УыКѓЃЌЕуPПЩвдзЗЩЯЕуQЃЛЃЈ3ЃЉЕуMЖдгІЕФЪ§ЪЧ-3![]() Лђ4ЃЎ
Лђ4ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРэНтгыећЪ§ЁЂЯрЗДЪ§ЁЂОјЖджЕгаЙиИХФюЃЌФмЙЛе§ШЗЛГіЪ§жсЃЌе§ШЗдкЪ§жсЩЯевЕНЫљЖдгІЕФЕуЃЛ
ЃЈ2ЃЉИљОнЪ§жсЩЯСНЕуМфЕФОрРыЕФЧѓЗЈНјааЧѓНтЃЛ
ЃЈ3ЃЉзЂвтЪ§жсЩЯСНЕуМфЕФОрРыЙЋЪНЃКСНЕуЫљЖдгІЕФЪ§ЕФВюЕФОјЖджЕЃЎ
ЃЈ1ЃЉaЪЧзюДѓЕФИКећЪ§ЃЌМДa=-1ЃЛ
bЪЧ-5ЕФЯрЗДЪ§ЃЌМДb=5ЃЌ
c=-|-2|=-2ЃЌ
ЫљвдЕуAЁЂBЁЂCдкЪ§жсЩЯЮЛжУШчЭМЫљЪОЃК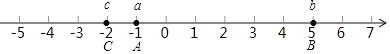
ЃЈ2ЃЉЩшдЫЖЏtУыКѓЃЌЕуPПЩвдзЗЩЯЕуQЃЌ
дђЕуPБэЪОЪ§-1+3tЃЌЕуQБэЪО5+tЃЌ
вРЬтвтЕУЃК-1+3t=5+tЃЌ
НтЕУЃКt=3ЃЎ
Д№ЃКдЫЖЏ3УыКѓЃЌЕуPПЩвдзЗЩЯЕуQЃЛ
ЃЈ3ЃЉДцдкЕуMЃЌЪЙMЕНAЁЂBЁЂCШ§ЕуЕФОрРыжЎКЭЕШгк12ЃЌa=-1ЃЌb=5ЃЌc=-2ЃЌ
ЕБMдкCЕузѓВрЃЌдђMЖдгІЕФЪ§ЪЧЃК-1-m+5-m-2-m=12,m=-3![]() ЃЛ
ЃЛ
ЕБMдкABжЎМфЃЌдђMЖдгІЕФЪ§ЪЧ:m+2+m+1+5-m=12,m=4ЃЎ
ЙЪЪЙЕуMЕНAЁЂBЁЂCШ§ЕуЕФОрРыжЎКЭЕШгк12ЃЌЕуMЖдгІЕФЪ§ЪЧ-3![]() Лђ4ЃЎ
Лђ4ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
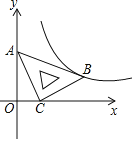
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌНЋвЛПщКЌга45ЁуНЧЕФжБНЧШ§НЧАхШчЭМЗХжУЃЌжБНЧЖЅЕуCЕФзјБъ(1,0)ЃЌЖЅЕуAЕФзјБъЮЊ(0, 2)ЃЌЖЅЕуBЧЁКУТфдкЕквЛЯѓЯоЕФЫЋЧњЯпЩЯЃЌЯжНЋжБНЧШ§НЧАхбиxжсе§ЗНЯђЦНвЦЃЌЕБЖЅЕуAЧЁКУТфдкИУЫЋЧњЯпЩЯЪБЭЃжЙдЫЖЏЃЌдђДЫЪБЕуCЕФЖдгІЕу
жаЃЌНЋвЛПщКЌга45ЁуНЧЕФжБНЧШ§НЧАхШчЭМЗХжУЃЌжБНЧЖЅЕуCЕФзјБъ(1,0)ЃЌЖЅЕуAЕФзјБъЮЊ(0, 2)ЃЌЖЅЕуBЧЁКУТфдкЕквЛЯѓЯоЕФЫЋЧњЯпЩЯЃЌЯжНЋжБНЧШ§НЧАхбиxжсе§ЗНЯђЦНвЦЃЌЕБЖЅЕуAЧЁКУТфдкИУЫЋЧњЯпЩЯЪБЭЃжЙдЫЖЏЃЌдђДЫЪБЕуCЕФЖдгІЕу![]() ЕФзјБъЮЊ__________
ЕФзјБъЮЊ__________
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЮФОпЕъЃЌМзжжБЪМЧБОБъМлУПБО8дЊЃЌввжжБЪМЧБОБъМлУПБО5дЊЃЎНёЬьЃЌМзЁЂввСНжжБЪМЧБОКЯМЦТєСЫ100БОЃЌЙВТєСЫ695дЊ!
ЃЈ1ЃЉСНжжБЪМЧБОИїЯњЪлСЫЖрЩйЃП
ЃЈ2ЃЉЫљЕУЯњЪлПюПЩФмЪЧ660дЊТ№ЃПЮЊЪВУДЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
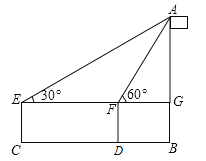
ЁОЬтФПЁПШчЭМЃЌаЁРізМБИВтвЛИљЦьИЫABЕФИпЖШЃЌвбжЊаЁРіЕФблОІРыЕиУцЕФОрРыEC=1.5УзЃЌЕквЛДЮВтСПЕуCКЭЕкЖўДЮВтСПЕуDжЎМфЕФОрРыCD=10УзЃЌЁЯAEG=30ЁуЃЌЁЯAFG=60ЁуЃЌЧыФуАяаЁРіМЦЫуГіетИљЦьИЫЕФИпЖШЃЎЃЈНсЙћБЃСєИљКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
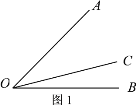
ЁОЬтФПЁПШчЭМ 1ЃЌЩфЯп OCдкЁЯAOBЕФФкВПЃЌЭМжаЙВга 3ИіНЧЃКЁЯAOBЁЂЁЯAOC КЭЁЯBOCЃЌШєЦфжагавЛИіНЧЕФЖШЪ§ЪЧСэвЛИіНЧЖШЪ§ЕФСНБЖЃЌдђГЦЩфЯп OCЪЧЁЯAOBЕФЦцУюЯпЃЎ
ЃЈ1ЃЉвЛИіНЧЕФНЧЦНЗжЯп_______етИіНЧЕФЦцУюЯпЃЎЃЈЬюЪЧЛђВЛЪЧЃЉЃЛ
ЃЈ2ЃЉШчЭМ 2ЃЌШєЁЯMPNЃН60ЁуЃЌЩфЯп PQШЦЕу PДг PNЮЛжУПЊЪМЃЌвдУПУы 10ЁуЕФЫйЖШФцЪБеыа§зЊЃЌЕБЁЯQPNЪзДЮЕШгк 180ЁуЪБЭЃжЙа§зЊЃЌЩша§зЊЕФЪБМфЮЊ tЃЈsЃЉЃЎ
Ђй ЕБ tЮЊКЮжЕЪБЃЌЩфЯп PMЪЧЁЯQPN ЕФЦцУюЯпЃП
ЂкШєЩфЯп PM ЭЌЪБШЦЕу PвдУПУы 5ЁуЕФЫйЖШФцЪБеыа§зЊЃЌВЂгы PQЭЌЪБЭЃжЙа§зЊЃЎЧыЧѓГіЕБЩфЯп PQЪЧЁЯMPNЕФЦцУюЯпЪБ tЕФжЕЃЎ


ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙѓГЩИпЬњПЊЭЈКѓМЋДѓЕиЗНБуСЫШЫУЧЕФГіааЃЌМзЁЂввСНИіГЧЪаЯрОр450ЧЇУзЃЌМгПЊИпЬњСаГЕКѓЃЌИпЬњСаГЕааЪЛЪБМфБШдЬиПьСаГЕааЪЛЪБМфЫѕЖЬСЫ3аЁЪБЃЌвбжЊИпЬњСаГЕЦНОљааЪЛЫйЖШЪЧдЬиПьСаГЕЦНОљааЪЛЫйЖШЕФ3БЖЃЌЧѓИпЬњСаГЕЕФЦНОљааЪЛЫйЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЬНЫїаТжЊЃЉ
ШчЭМ1ЃЌЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЃЌЭМжаЙВга3ЬѕЯпЖЮЃК
ЩЯЃЌЭМжаЙВга3ЬѕЯпЖЮЃК![]() ЁЂ
ЁЂ![]() КЭ
КЭ![]() ЃЌШєЦфжагавЛЬѕЯпЖЮЕФГЄЖШЪЧСэвЛЬѕЯпЖЮГЄЖШЕФСНБЖЃЌдђГЦЕу
ЃЌШєЦфжагавЛЬѕЯпЖЮЕФГЄЖШЪЧСэвЛЬѕЯпЖЮГЄЖШЕФСНБЖЃЌдђГЦЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЕФЁАЖўБЖЕуЁБ.
ЕФЁАЖўБЖЕуЁБ.
ЃЈ1ЃЉЂйвЛЬѕЯпЖЮЕФжаЕу етЬѕЯпЖЮЕФЁАЖўБЖЕуЁБЃЛЃЈЬюЁАЪЧЁБЛђЁАВЛЪЧЁБЃЉ
ЂкШєЯпЖЮ![]() ЃЌ
ЃЌ![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЕФЁАЖўБЖЕуЁБЃЌдђ
ЕФЁАЖўБЖЕуЁБЃЌдђ![]() ЃЈаДГіЫљгаНсЙћЃЉ
ЃЈаДГіЫљгаНсЙћЃЉ
ЃЈЩюШыбаОПЃЉ
ШчЭМ2ЃЌШєЯпЖЮ![]() ЃЌЕу
ЃЌЕу![]() ДгЕу
ДгЕу![]() ЕФЮЛжУПЊЪМЃЌвдУПУы2
ЕФЮЛжУПЊЪМЃЌвдУПУы2![]() ЕФЫйЖШЯђЕу
ЕФЫйЖШЯђЕу![]() дЫЖЏЃЌЕБЕу
дЫЖЏЃЌЕБЕу![]() ЕНДяЕу
ЕНДяЕу![]() ЪБЭЃжЙдЫЖЏЃЌдЫЖЏЕФЪБМфЮЊ
ЪБЭЃжЙдЫЖЏЃЌдЫЖЏЕФЪБМфЮЊ![]() Уы.
Уы.
ЃЈ2ЃЉЮЪ![]() ЮЊКЮжЕЪБЃЌЕу
ЮЊКЮжЕЪБЃЌЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЕФЁАЖўБЖЕуЁБЃЛ
ЕФЁАЖўБЖЕуЁБЃЛ
ЃЈ3ЃЉЭЌЪБЕу![]() ДгЕу
ДгЕу![]() ЕФЮЛжУПЊЪМЃЌвдУПУы1
ЕФЮЛжУПЊЪМЃЌвдУПУы1![]() ЕФЫйЖШЯђЕу
ЕФЫйЖШЯђЕу![]() дЫЖЏЃЌВЂгыЕу
дЫЖЏЃЌВЂгыЕу![]() ЭЌЪБЭЃжЙ.ЧыжБНгаДГіЕу
ЭЌЪБЭЃжЙ.ЧыжБНгаДГіЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЕФЁАЖўБЖЕуЁБЪБ
ЕФЁАЖўБЖЕуЁБЪБ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЃКЃЈ1ЃЉ13+ЃЈЃ18ЃЉЃЃЈ6Ѓ11ЃЉ
ЃЈ2ЃЉ![]() ЁТ
ЁТ![]()
ЃЈ3ЃЉЃ14Ѓ![]() ЁС[2Ѓ(Ѓ3)2]
ЁС[2Ѓ(Ѓ3)2]
ЃЈ4ЃЉaЃ2bЃ[Ѓ4aЃЋ(cЃЋ3b)]
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФЗНГЬx2ЉЃЈm+n+1ЃЉx+mЃЈnЁн0ЃЉЕФСНИіЪЕЪ§ИљЮЊІСЁЂІТЃЌЧвІСЁмІТЃЎ
ЃЈ1ЃЉЪдгУКЌІСЁЂІТЕФДњЪ§ЪНБэЪОmКЭnЃЛ
ЃЈ2ЃЉЧѓжЄЃКІСЁм1ЁмІТЃЛ
ЃЈ3ЃЉШєЕуPЃЈІСЃЌІТЃЉдкЁїABCЕФШ§ЬѕБпЩЯдЫЖЏЃЌЧвЁїABCЖЅЕуЕФзјБъЗжБ№ЮЊAЃЈ1ЃЌ2ЃЉЁЂBЃЈ![]() ЃЌ1ЃЉЁЂCЃЈ1ЃЌ1ЃЉЃЌЮЪЪЧЗёДцдкЕуPЃЌЪЙm+n=
ЃЌ1ЃЉЁЂCЃЈ1ЃЌ1ЃЉЃЌЮЪЪЧЗёДцдкЕуPЃЌЪЙm+n=![]() ЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com