
如图,一块三角形铁皮,其中∠B=30°,∠C=45°,AC=12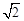 cm, 工人师傅利用这块铁皮做了一个侧面积最大的圆锥,求这个圆锥的底面直径.
cm, 工人师傅利用这块铁皮做了一个侧面积最大的圆锥,求这个圆锥的底面直径.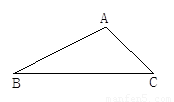
4cm
【解析】
试题分析:过A作AD⊥BC,则由∠C=45°得AD=DC=12cm,AB=2AD=24cm,根据勾股定理可得BD的长,从而可得BC的长,求得以A为圆心的扇形面积,以B为圆心的扇形面积,以C为圆心的扇形面积,比较即可判断,最后根据圆周长公式结合弧长公式即可求得结果.
过A作AD⊥BC
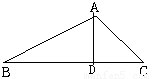
则由∠C=45°得AD=DC=12cm,AB=2AD=24cm
BD=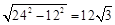 ,从而BC=
,从而BC=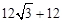
以A为圆心的扇形面积为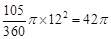 cm2
cm2
以B为圆心的扇形面积为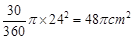
以C为圆心的扇形面积为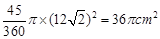
故以B为圆心取扇形作圆锥侧面时,圆锥的侧面积最大,
设此时圆锥的底面半径为r
则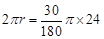 ,解得r=2cm
,解得r=2cm
答:这个圆锥的底面直径为4cm.
考点:勾股定理,扇形面积公式,圆周长公式,弧长公式
点评:辅助线问题是初中数学的难点,能否根据题意准确作出适当的辅助线很能反映一个学生的对图形的理解能力,因而是中考的热点,尤其在压轴题中比较常见,需特别注意.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:
 如图,有一块三角形铁皮余料ABC,∠C=90°,BC=60cm,AC=40cm,现要在这块三角形铁皮余料截出一个最大的正方形PQCR,正方形PQCR的边长是多少?
如图,有一块三角形铁皮余料ABC,∠C=90°,BC=60cm,AC=40cm,现要在这块三角形铁皮余料截出一个最大的正方形PQCR,正方形PQCR的边长是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,有一块三角形铁皮余料ABC,∠C=90°,BC=60cm,AC=40cm,现要在这块三角形铁皮余料截出一个最大的正方形PQCR,正方形PQCR的边长是多少?
如图,有一块三角形铁皮余料ABC,∠C=90°,BC=60cm,AC=40cm,现要在这块三角形铁皮余料截出一个最大的正方形PQCR,正方形PQCR的边长是多少?查看答案和解析>>
科目:初中数学 来源: 题型:
有一块三角形铁皮ABC,最长边BC=12cm,高AD=8cm,要把它加工成一个矩形铁片,使矩形的一边在BC上,其余两个顶点分别在AB.AC上,且矩形的长是宽的2倍,现有两种加工方案,如图,问:哪个方案加工成的矩形铁片面积较大。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com