
【题目】某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
求每台电冰箱与空调的进价分别是多少?
(2)现在商城准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13000元,请分析合理的方案共有多少种?并确定获利最大的方案以及最大利润.
【答案】(1)每台空调的进价为1600元,则每台电冰箱的进价为2000元.
(2)当购进电冰箱34台,空调66台获利最大,最大利润为13300元.
【解析】试题分析:(1)分式方程中的销售问题,题目中有两个相等关系,①每台电冰箱的进价比每台空调的进价多400元,用80000元购进电冰箱的数量与用64000元购进空调的数量相等,用第一个相等关系,设每台空调的进价为m元,表示出每台电冰箱的进价为(m+400)元,用第二个相等关系列方程: ![]() .
.
(2)销售问题中的确定方案和利润问题,题目中有两个不等关系,①要求购进空调数量不超过电冰箱数量的2倍,②总利润不低于13000元,根据题意设出设购进电冰箱x台(x为正整数),这100台家电的销售总利润为y元,列出不等式组![]() ,确定出购买电冰箱的台数的范围,从而确定出购买方案,再利用一次函数的性质确定出,当x=34时,y有最大值,即可.
,确定出购买电冰箱的台数的范围,从而确定出购买方案,再利用一次函数的性质确定出,当x=34时,y有最大值,即可.
试题解析:
(1)设每台空调的进价为x元,则每台电冰箱的进价为(x+400)元,根据题意得:
![]() ,
,
解得:x=1600,
经检验,x=1600是原方程的解
∴x+400=1600+400=2000,
答:每台空调的进价为1600元,则每台电冰箱的进价为2000元.
(2)设购进电冰箱x台,这100台家电的销售总利润为y元,
则y=(2100﹣2000)x+(1750﹣1600)(100﹣x)=﹣50x+15000,
根据题意得: ![]() ,
,
解得: ![]() ,
,
∵x为正整数,
∴x=34,35,36,37,38,39,40,
∴合理的方案共有7种.
∵y=﹣50x+15000,k=﹣50<0,
∴y随x的增大而减小,
∴当x=34时,y有最大值,最大值为:﹣50×34+15000=13300(元),
答:当购进电冰箱34台,空调66台获利最大,最大利润为13300元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】线段EF是由线段PQ平移得到的,点P(﹣1,4)的对应点为E(4,7),则点Q(﹣3,1)的对应点F的坐标为()
A.(﹣8,﹣2)
B.(﹣2,﹣2)
C.(2,4)
D.(﹣6,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种生物孢子的直径为0.000 63m,用科学记数法表示为( )
A.0.63×10﹣3m
B.6.3×10﹣4m
C.6.3×10﹣3m
D.6.3×10﹣5m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,直线EF分别与AB,CD交于点G,H,GM⊥EF,HN⊥EF,交AB于点N,∠1=50°. 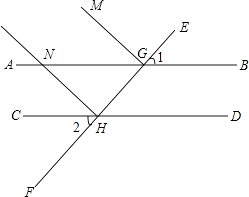
(1)求∠2的度数;
(2)试说明HN∥GM;
(3)∠HNG=°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,∠A=∠D,试说明 AC∥DE 成立的理由.
(下面是彬彬同学进行的推理,请你将彬彬同学的推理过程补充完整.)
解:∵AB∥CD (已知)
∴∠A=(两直线平行,内错角相等)
又∵∠A=∠D()
∴∠=∠(等量代换)
∴AC∥DE ()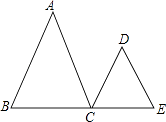
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com