
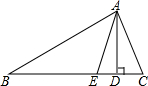
 已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠ABC=30°,∠ACB=50°.
已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠ABC=30°,∠ACB=50°.分析 (1)先根据三角形内角和得到∠CAB=180°-∠B-∠C=100°,再根据角平分线与高线的定义得到∠CAE=$\frac{1}{2}$∠CAB=50°,∠ADC=90°,则∠CAD=90°-∠C=40°,然后利用∠DAE=∠CAE-∠CAD计算即可.
(2)根据题意可以用∠B和∠C表示出∠CAD和∠CAE,从而可以得到∠DAE与∠C-∠B的关系.
解答  解:∵∠ABC=30°,∠ACB=50°,
解:∵∠ABC=30°,∠ACB=50°,
∴∠CAB=180°-∠B-∠C=100°,
∵AE是△ABC角平分线,
∴∠CAE=$\frac{1}{2}$∠CAB=50°,
∵AD分别是△ABC的高,
∴∠ADC=90°,
∴∠CAD=90°-∠C=40°,
∴∠DAE=∠CAE-∠CAD=50°-40°=10°.
(2)∠DAE=$\frac{1}{2}$(∠ACB-∠ABC),
理由:∵在△ABC中,AD,AE分别是△ABC的高和角平分线,
∴∠CAB=180°-∠B-∠C,∠CAD=90°-∠C,∠CAE=$\frac{1}{2}$(180°-∠B-∠C),
∴∠DAE=$\frac{1}{2}$(180°-∠B-∠C)-(90°-∠C)=$\frac{1}{2}$(∠C-∠B).
故答案为:∠DAE=$\frac{1}{2}$(∠ACB-∠ABC).
点评 本题考查三角形内角和定理、角的平分线的性质、直角三角形的性质,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-(b+c)=a-b+c | B. | a+b-c=a+(b-c) | C. | a+(b+c)=a-b+c | D. | a+b-c=a-(b+c) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
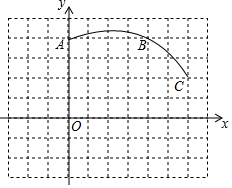 如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号):
如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号):查看答案和解析>>
科目:初中数学 来源: 题型:解答题
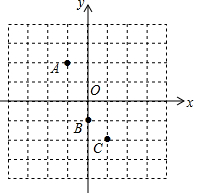 如图,已知二次函数y=ax2+bx+c的图象经过A (-1,2)、B (0,-1)、C (1,-2).
如图,已知二次函数y=ax2+bx+c的图象经过A (-1,2)、B (0,-1)、C (1,-2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -(2a+b-c)=2a+b-c | B. | -2(a+b-4c)=-2a-2b+8c | ||
| C. | -(-a-b+2c)=-a+b+2c | D. | -(a-b-c)=-a+b-c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
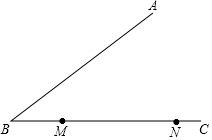 如图,点M、N是∠ABC的边BC上不重合的两点.请你利用直尺与圆规在平面上画出点P,使得点P到边BA、BC的距离相等,且∠MPN=90°.(保留作图痕迹)
如图,点M、N是∠ABC的边BC上不重合的两点.请你利用直尺与圆规在平面上画出点P,使得点P到边BA、BC的距离相等,且∠MPN=90°.(保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,3) | B. | (-3,3) | C. | (-3,-3) | D. | (3,-3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com