
【题目】如图,钓鱼竿AC长6m,露在水面上的鱼线BC长3![]() m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到AC′的位置,此时露在水面上的鱼线B′C′为3
m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到AC′的位置,此时露在水面上的鱼线B′C′为3![]() m,则鱼竿转过的角度是__________.
m,则鱼竿转过的角度是__________.

【答案】15°
【解析】分析:根据图示可得:在Rt△ABC中,由勾股定理可得:![]() ,可得AB=BC,所以∠CAB=45°, Rt△AB’C’中,由勾股定理可得:
,可得AB=BC,所以∠CAB=45°, Rt△AB’C’中,由勾股定理可得:![]() ,可得AB’=
,可得AB’=![]() AC’,根据在直角三角形中,30°角所对直角边等于斜边的一半可得, ∠AC’B’=30°,继而可得∠C’AB‘=60°,即∠C’AC=15°.
AC’,根据在直角三角形中,30°角所对直角边等于斜边的一半可得, ∠AC’B’=30°,继而可得∠C’AB‘=60°,即∠C’AC=15°.
详解: 在Rt△ABC中,由勾股定理可得:
![]() ,
,
所以AB=BC,
所以∠CAB=45°,
在Rt△AB’C’中,由勾股定理可得:![]() ,
,
所以AB’=![]() AC’,
AC’,
根据在直角三角形中,30°角所对直角边等于斜边的一半可得, ∠AC’B’=30°,
所以∠C’AB‘=60°,
∠C’AC=60°-45°=15°,故答案为:15°.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】一个自然数的立方,可以分裂成若干个连续奇数的和,例如:23,33和43分别可以按如图所示的方式“分裂”,则63“分裂”出的奇数中,最大的奇数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要将一块长为a米,宽为b米的长方形空地设计成花园,现有如下两种方案供选择.
方案一:如图1,在空地上横、竖各铺一条宽为4米的石子路,其余空地种植花草.
方案二:如图2,在长方形空地中留一个四分之一圆和一个半圆区域种植花草,其余空地铺筑成石子路.
(1) 分别表示这两种方案中石子路(图中阴影部分)的面积(若结果中含有π,则保留)
(2) 若a=30,b=20,该校希望多种植物美化校园,请通过计算选择其中一种方案(π取3.14).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac;②2a+b=0;③a﹣b+c=0;④5a<b.其中正确结论是( ) 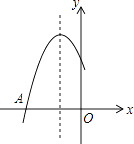
A.②④
B.①④
C.②③
D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是一张纸片,∠C=90°,AC=6,BC=8,现将其折叠.使点B与点A重合,折痕为DE,则DE的长为( )
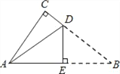
A. 1.75 B. 3 C. 3.75 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的情况(记向东为正)记录如下(x>5且x<14,单位:m):
行驶次数 | 第一次 | 第二次 | 第三次 | 第四次 |
行驶情况 | x | ﹣ | x﹣3 | 2(5﹣x) |
行驶方向(填“东”或“西”) |
|
|
|
|
(1)请将表格补充完整;
(2)求经过连续4次行驶后,这辆出租车所在的位置;
(3)若出租车行驶的总路程为41m,求第一次行驶的路程x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某网店的“翻牌抽奖”活动,如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品. 
(1)如果随机翻1张牌,那么抽中20元奖品的概率为 .
(2)如果随机翻2张牌,且第一次翻过的牌不再参加下次翻牌,请用列表或画树状图的方法求出所获奖品总值不低于30元的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鸡兔同笼问题是我国古代著名趣题之一,大约在 1500 年前,《孙子算经》中就记载了这个有趣的问题.书中是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡、兔同在一个笼子里,从上上面数,有 35 个头;从下面数,有 94 只脚 .求笼中各有几只鸡和兔?经计算可得( )

A. 鸡 20 只,兔 15 只 B. 鸡 12 只,兔 23 只
C. 鸡 15 只,兔 20 只 D. 鸡 23 只,兔 12 只
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边AB在x轴上,点B与原点O重合,已知点A(﹣2,0),AC= ![]() ,将△ABC沿x轴向右平移,当点C的对应点C1落在直线y=2x﹣4上时,则平移的距离是( )
,将△ABC沿x轴向右平移,当点C的对应点C1落在直线y=2x﹣4上时,则平移的距离是( )
A.2
B.3
C.4
D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com