Question

如图，D、E分别为△ABC的AC，BC边的中点，将此三角形沿DE折叠，使点C落在AB边上的点P处，若∠A=46°，有下列结论：①DE∥AB；②∠APD=46°；③∠ADP=88°；④△PEB是等腰三角形，正确的是________．（只需填写序号）

Answer 1

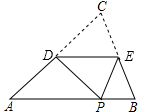
①②③④
分析：由中位线定理得DE∥AB，由翻折定理可知△PED≌△CED，可得CD=PD，CE=PE，即可求出∠APD，∠ADP，也可判定△PEB是等腰三角形．
解答：∵D、E分别为△ABC的AC，BC边的中点，
∴DE是△ABC的中位线，
∴DE∥AB，
∵△PED是△CED翻折变换来的，
∴△PED≌△CED，
∴CD=PD，CE=PE，
∵CD=DA，
∴DA=DP，
∴∠APD=∠A=46°，
∴∠ADP=180°-46°-46°=88°，
∵E为BC中点，
∴CE=EB，
∵CE=PE，
∴PE=EB，
∴△PEB是等腰三角形．
故答案为①②③④．
点评：本题考查三角形中位线定理的位置关系，并运用了三角形的翻折变换知识，解答此题的关键是要了解图形翻折变换后与原图形全等．