

分析 (1)如图①,根据等腰直角三角形的性质得∠ABC=45°,再根据旋转的性质得∠BAD=∠CAE=30°,AB=AD,AC=AE,∠ADE=∠ABC=45°,∠AED=∠ACB=90°,则利用等腰三角形的性质得∠ABD=∠ADB,∠ACE=∠AEC,然后根据三角形捏角和定理可计算出∠ADB=∠AEC=75°,根据互余计算出∠OED=15°,再利用三角形外角和性质可计算出∠BOE=∠ODE+∠OED=135°;
(2)如图②,根据旋转的性质得∠BAD=∠CAE=θ,AB=AD,AC=AE,∠ADE=∠ABC=45°,∠AED=∠ACB=90°,则利用等腰三角形的性质得∠ABD=∠ADB,∠ACE=∠AEC,接着根据三角形内角和定理可计算出∠ADB=90°-$\frac{1}{2}$θ,∠AEC=90°-$\frac{1}{2}$θ,利用互余计算出∠OED=∠AED-∠AEC=$\frac{1}{2}$θ,然后利用三角形外角和性质可计算出∠BOE=∠ODE+∠OED=135°.
解答 解:(1)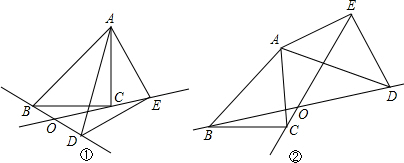 如图①,
如图①,
∵△ABC是等腰直角三角形,∠ACB=90°,
∴∠ABC=45°,
∵△ABC绕点A逆时针旋转30°得△ADE,
∴∠BAD=∠CAE=30°,AB=AD,AC=AE,∠ADE=∠ABC=45°,∠AED=∠ACB=90°,
∴∠ABD=∠ADB,∠ACE=∠AEC,
∴∠ADB=$\frac{1}{2}$(180°-30°)=75°,∠AEC=$\frac{1}{2}$(180°-30°)=75°,
∴∠OED=∠AED-∠AEC=90°-75°=15°,
∴∠BOE=∠ODE+∠OED=75°+45°+15°=135°,
故答案为135;
(2)∠BOE的度数与(1)中的结果相同.理由如下:
如图②,
∵△ABC是等腰直角三角形,∠ACB=90°,
∴∠ABC=45°,
∵△ABC绕点A逆时针旋转θ得△ADE,
∴∠BAD=∠CAE=θ,AB=AD,AC=AE,∠ADE=∠ABC=45°,∠AED=∠ACB=90°,
∴∠ABD=∠ADB,∠ACE=∠AEC,
∴∠ADB=$\frac{1}{2}$(180°-θ)=90°-$\frac{1}{2}$θ,∠AEC=90°-$\frac{1}{2}$θ,
∴∠OED=∠AED-∠AEC=90°-(90°-$\frac{1}{2}$θ)=$\frac{1}{2}$θ,
∴∠BOE=∠ODE+∠OED=90°-$\frac{1}{2}$θ+45°+$\frac{1}{2}$θ=135°,
即∠BOE的度数与(1)中的结果相同.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的性质和等腰三角形的性质.


科目:初中数学 来源: 题型:选择题
| A. | 一个游戏的中奖概率是$\frac{1}{10}$,则做10次这样的游戏一定会中奖 | |
| B. | 为了解全国中学生的心理健康情况,适合采用抽样调查的方式 | |
| C. | 为了解某市九年级学生的肺活量,从中抽样调查了500名学生的肺活量,这项调查中的样本是从中抽取的500名学生 | |
| D. | 若甲组数据的方差S2=0.01,乙组数据的方差S2=0.1,则乙组数据比甲组数据稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{5}$,下列结论:①△APD≌△AEB;②点B到直线AE的距离为$\sqrt{2}$;③EB⊥ED;④S△APD+S△APB=$\frac{1+\sqrt{6}}{2}$.其中正确结论的序号是①③④.
已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{5}$,下列结论:①△APD≌△AEB;②点B到直线AE的距离为$\sqrt{2}$;③EB⊥ED;④S△APD+S△APB=$\frac{1+\sqrt{6}}{2}$.其中正确结论的序号是①③④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
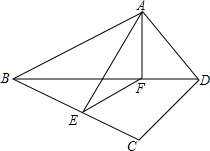 已知:四边形ABCD中,AD=CD,对角线BD平分∠ADC,点E,F分别是线段BC和线段BD上的点,且点F在线段EC的垂直平分线上,连接EF,AF,AE.
已知:四边形ABCD中,AD=CD,对角线BD平分∠ADC,点E,F分别是线段BC和线段BD上的点,且点F在线段EC的垂直平分线上,连接EF,AF,AE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com