
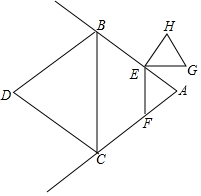
 如图,在∠BAC中,分别以AB,AC为邻边构造周长为20的菱形ABDC,且BC=6,EF∥BC分别交射线AB,AC于点E,F,将△AEF绕点E逆时针旋转90°得到△HEG(A和H,F和G分别是对顶点).点E从点A出发沿射线AB方向运动,设AE=t.
如图,在∠BAC中,分别以AB,AC为邻边构造周长为20的菱形ABDC,且BC=6,EF∥BC分别交射线AB,AC于点E,F,将△AEF绕点E逆时针旋转90°得到△HEG(A和H,F和G分别是对顶点).点E从点A出发沿射线AB方向运动,设AE=t.分析 (1))由EF∥BC,推出$\frac{EF}{BC}$=$\frac{AE}{AB}$,考点$\frac{EF}{6}$=$\frac{t}{5}$,求出EF即可解决问题.
(2)①如图1中,连接AD交BD于O,设⊙B与直线NR相切于点M,连接BM,NR交AC于K.由图象可知,当点E与N重合时,EG的值最大,最大值为NK,想办法求出NK即可.②分两种情形考虑问题,当BO-EL=2或EL-BO=2时,直线EG与⊙B相切,构建方程即可解决问题,因为EH⊥AB,观察图象可知当t=3或7时,直线EH与⊙B相切.
(3)如图3中,易知点G在射线AG上运动,作GN⊥AE于N,BK⊥AG于K.在Rt△EGN中,由EG=$\frac{6}{5}$t,tan∠EGN=$\frac{3}{4}$,推出GN=$\frac{18}{25}$t,EN=$\frac{24}{25}$t,推出AN=$\frac{1}{25}$t,在Rt△AGN中,AG=$\sqrt{N{G}^{2}+A{N}^{2}}$=$\frac{\sqrt{13}}{5}$t,推出sin∠EAG=$\frac{GN}{AG}$=$\frac{\frac{24}{25}t}{\frac{\sqrt{13}}{5}t}$=$\frac{24}{65}$$\sqrt{13}$,在Rt△ABK中,BK=AB•sin∠EAG=$\frac{24}{13}$$\sqrt{13}$,根据垂线段最短可知,当点G与K重合时,QG的值最小,由此即可解决问题.
解答 解:(1)∵EF∥BC,
∴$\frac{EF}{BC}$=$\frac{AE}{AB}$,
∴$\frac{EF}{6}$=$\frac{t}{5}$,
∴EF=$\frac{6}{5}$t,
∴EG=EF=$\frac{6}{5}$t.
(2)①如图1中,连接AD交BD于O,设⊙B与直线NR相切于点M,连接BM,NR交AC于K.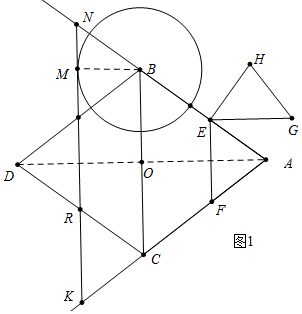
由图象可知,当点E与N重合时,EG的值最大,最大值为NK,
易知△BMN∽△AOB,
∴$\frac{BN}{AB}$=$\frac{BM}{OA}$,
∴$\frac{BN}{5}$=$\frac{2}{4}$,
∴BN=$\frac{5}{2}$,
∴AN=$\frac{15}{2}$,
∵BC∥NK,
∴$\frac{BC}{NK}$=$\frac{AB}{AN}$,
∴$\frac{6}{NK}$=$\frac{5}{\frac{15}{2}}$,
∴NK=9,
∴EG的最大值为9.
②如图2中,设EF交AD于L,则EL=$\frac{3}{5}$t,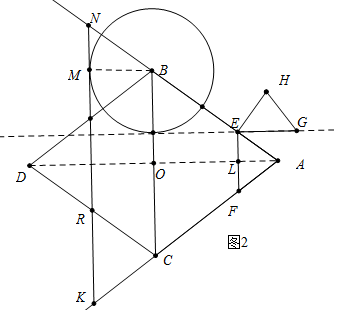
当BO-EL=2或EL-BO=2时,直线EG与⊙B相切,
即3-$\frac{3}{5}\\;t$t=2或$\frac{3}{5}$t-3=2,
解得t=$\frac{5}{3}$或$\frac{25}{3}$,
∵EH⊥AB,
∴当t=3或7时,直线EH与⊙B相切,
综上所述,当t=3s或7s或$\frac{5}{3}$s或$\frac{25}{3}$s时,⊙B与△HEG的边EG或EH所在的直线相切
(3)如图3中,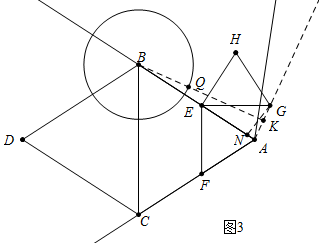
易知点G在射线AG上运动,作GN⊥AE于N,BK⊥AG于K.
在Rt△EGN中,∵EG=$\frac{6}{5}$t,tan∠EGN=$\frac{3}{4}$,
∴GN=$\frac{18}{25}$t,EN=$\frac{24}{25}$t,
∴AN=$\frac{1}{25}$t,
在Rt△AGN中,AG=$\sqrt{N{G}^{2}+A{N}^{2}}$=$\frac{\sqrt{13}}{5}$t,
∴sin∠EAG=$\frac{GN}{AG}$=$\frac{\frac{24}{25}t}{\frac{\sqrt{13}}{5}t}$=$\frac{24}{65}$$\sqrt{13}$,
在Rt△ABK中,BK=AB•sin∠EAG=$\frac{24}{13}$$\sqrt{13}$,
根据垂线段最短可知,当点G与K重合时,QG的值最小,最小值=$\frac{24}{13}$$\sqrt{13}$-2.
故答案为$\frac{24}{13}$$\sqrt{13}$-2.
点评 本题考查圆综合题、菱形的性质、平行线分线段成比例定理、垂线段最短、相似三角形的判定和性质、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,学会用构建方程的思想思考问题,灵活应用垂线段最短解决最值问题,属于中考压轴题.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
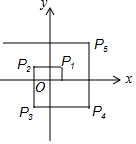 如图,在直角坐标系中,设一动点自P0(1,0)处向上运动1个单位长度至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,…如此继续运动下去,设Pn(xn,yn),n=1,2,3,…则x1+x2+…+x99+x100=( )
如图,在直角坐标系中,设一动点自P0(1,0)处向上运动1个单位长度至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,…如此继续运动下去,设Pn(xn,yn),n=1,2,3,…则x1+x2+…+x99+x100=( )| A. | 0 | B. | -49 | C. | 50 | D. | -50 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
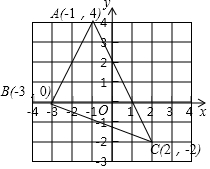 如图,三角形ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+3,y0-1),将三角形ABC作同样的平移得到三角形A1B1C1,则A1的坐标是( )
如图,三角形ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+3,y0-1),将三角形ABC作同样的平移得到三角形A1B1C1,则A1的坐标是( )| A. | (-4,3) | B. | (-4,5) | C. | (2,3) | D. | (2,5) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{800}{x+30}$=$\frac{600}{x}$ | B. | $\frac{800}{x-30}$=$\frac{600}{x}$ | C. | $\frac{800}{x}$=$\frac{600}{x+30}$ | D. | $\frac{800}{x}$=$\frac{600}{x-30}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | $\sqrt{3}$×$\sqrt{5}$=$\sqrt{15}$ | D. | $\sqrt{(-3)^{2}}$=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
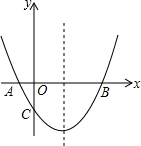 如图,抛物线经过A(-1,0),B(5,0),C(0,-$\frac{5}{2}$)三点.
如图,抛物线经过A(-1,0),B(5,0),C(0,-$\frac{5}{2}$)三点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com