
分析 (1)原方程有实数根,则△≥0.结合两根的积是两根和的2倍来求m的值;
(2)利用完全平方公式的变形公式解答.
解答 (1)解:由题意:△=(2m-1)2-4(m2+2)≥0,
∴4m+7≤0,
∴m≤$\frac{7}{4}$.
又x1+x2=-(2m-1),x1•x2=m2+2,x1•x2=2(x1+x2),
∴m2+2=-2(2m-1),
∴m2+4m=0,
∴m1=-4,m2=0(舍),
∴m=-4;
(2)解:由m=-4,得
x1+x2=-(2m-1)=9,x1•x2=m2+2=18,
∴|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=$\sqrt{{9}^{2}-4×18}$
=$\sqrt{9}$
=3.
点评 本题考查了根与系数的关系,根的判别式以及完全平方公式.解答(1)题时,注意m的取值还受约于根的判别式的符号.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
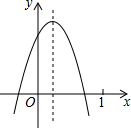 二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①ac<0;②方程ax2+bx+c=0的两根之和大于0;③y随x的增大而增大;④a-b+c<0.其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①ac<0;②方程ax2+bx+c=0的两根之和大于0;③y随x的增大而增大;④a-b+c<0.其中正确的是( )| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
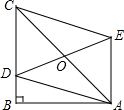 如图,在Rt△ABC中,∠B=90°,AB=10,BC>AB,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是10.
如图,在Rt△ABC中,∠B=90°,AB=10,BC>AB,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
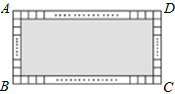 如图所示的是由一个小矩形与52个边长为1的小正方形组成的大矩形,小矩形的长与宽之比是7:5,若设小矩形的长为x,宽为y,则根据题意可列方程组( )
如图所示的是由一个小矩形与52个边长为1的小正方形组成的大矩形,小矩形的长与宽之比是7:5,若设小矩形的长为x,宽为y,则根据题意可列方程组( )| A. | $\left\{\begin{array}{l}{x:y=7:5}\\{2(x+y)+4=52}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x:y=5:7}\\{2(x+y)+4=52}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x:y=5:7}\\{x+y=52}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x:y=7:5}\\{2(x+y)=52}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
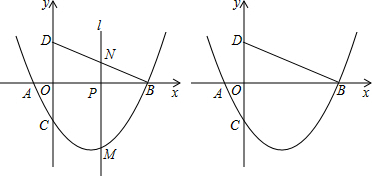
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,BO平分∠ABC,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=10,则△AMN的周长为( )
如图,BO平分∠ABC,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=10,则△AMN的周长为( )| A. | 22 | B. | 36 | C. | 46 | D. | 34 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com