
Ϊ�˴����������ij��У�ʵ����֦����Խʽ��չ�����л���������������Ͷ�ʼƻ������ƽ��������������蹤�̲������·������Ҫ������ʯ�����ƻ�ÿСʱ�ھ���ʯ��540m3���־�����ij���ͻ�е����˾���üס��������ͺŵ��ھ������������������˾�ṩ���ھ���й���Ϣ�����
|
| ��𣨵�λ��Ԫ/̨•ʱ�� | �ھ���ʯ��������λ��m3/̨•ʱ�� |
| �����ھ�� | 100 | 60 |
| �����ھ�� | 120 | 80 |
��1�������üס��������ͺŵ��ھ����8̨��ǡ�����ÿСʱ���ھ�������ס��������ͺŵ��ھ���������̨��
��2�����ÿСʱ֧���������850Ԫ����ǡ�����ÿСʱ���ھ�������ô���м��ֲ�ͬ�����÷�����
�⣺��1����ס��������ͺŵ��ھ������x̨��y̨��
������ã�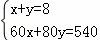 ��
��
��� 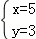 ��
��
�𣺼ס��������ͺŵ��ھ������5̨��3̨��
��2��������m�������ھ����n�������ھ����
������ã�60m+80n=540������ã�3m+4n=27��
��m=9��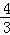 n��
n��
��̵Ľ�Ϊ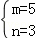 ��
��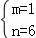 ��
��
��m=5��n=3ʱ��֧�����100��5+120��3=860Ԫ��850Ԫ�������
��m=1��n=6ʱ��֧�����100��1+120��6=820Ԫ������Ҫ��
����һ���������������1�������ھ����3�������ھ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
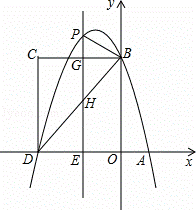
��ͼ����ƽ��ֱ������ϵ�У�������y=��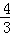 x2+bx+c��x�ύ��A��D���㣬��y�ύ�ڵ�B���ı���OBCD�Ǿ��Σ���A������Ϊ��1��0������B������Ϊ��0��4������֪��E��m��0�����߶�DO�ϵĶ��㣬����E��PE��x�ύ�������ڵ�P����BC�ڵ�G����BD�ڵ�H��
x2+bx+c��x�ύ��A��D���㣬��y�ύ�ڵ�B���ı���OBCD�Ǿ��Σ���A������Ϊ��1��0������B������Ϊ��0��4������֪��E��m��0�����߶�DO�ϵĶ��㣬����E��PE��x�ύ�������ڵ�P����BC�ڵ�G����BD�ڵ�H��
��1����������ߵĽ���ʽ��
��2������P��ֱ��BC�Ϸ�ʱ�����ú�m�Ĵ���ʽ��ʾPG�ij��ȣ�
��3���ڣ�2���������£��Ƿ���������ĵ�P��ʹ����P��B��GΪ��������������DEH���ƣ������ڣ������ʱm��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
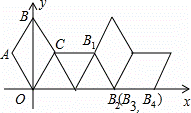
��ͼ������ϵ�з���һ����OABC����֪��ABC=60�㣬OA=1���Ƚ�����OABC��x���������������ת��ÿ�η�ת60�㣬������ת2014�Σ���B���������ΪB1��B2��B3��������B2014������Ϊ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��������ABCD�ı�CD��������CGEF�ı�CE�غϣ�O��EG���е㣬��EGC��������GH����D����BE��H������OH��FH��EG��FH����M�����������ĸ����ۣ�
��GH��BE����HO
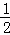 BG���۵�H����������CGFE�����Բ�ϣ��ܡ�GBE�ס�GMF��
BG���۵�H����������CGFE�����Բ�ϣ��ܡ�GBE�ס�GMF��
������ȷ�Ľ����У�������
| �� | A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���м�����ȷ���ǣ�������
�� A�� 3a��2a=1 B�� a2+a5=a7 C�� a2•a4=a6 D�� ��ab��3=ab3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
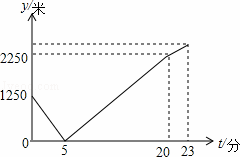
�糿��С������ͨ��ѧУΨһ��һ��·��ֱ·����ѧ��;�з����������У�ͣ���������绰������ӵ��绰����Ϸ������ϸ���ѧУ��ͬʱС�շ��أ�����������С����������ѧУ������ؼң�15�������赽�ң��پ���3����С�յ���ѧУ��С��ʼ����100��/�ֵ��ٶȲ��У�С�պ�����ľ���y����λ���ף���С�մ���绰��IJ���ʱ��t����λ���֣�֮��ĺ�����ϵ��ͼ����������˵����
�ٴ�绰ʱ��С�պ�����ľ���Ϊ1250�ף�
�ڴ���绰����23����С�յ���ѧУ��
��С�պ���������������ؼҵ��ٶ�Ϊ150��/�֣�
��С�ռ���ѧУ�ľ���Ϊ2550�ף�������ȷ�ĸ����ǣ�������
�� A�� 1�� B�� 2�� C�� 3�� D�� 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
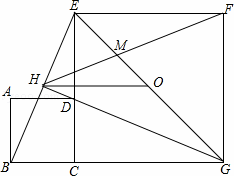
��ͼ����ƽ��ֱ�������У���OΪ����ԭ�㣬ֱ��y=��x+4��x�ύ�ڵ�A������A��������y=ax2+bx��ֱ��y=��x+4������һ��B���ҵ�B�ĺ�����Ϊ1��
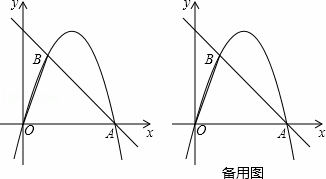
��1����a��b��ֵ��
��2����P���߶�AB��һ���㣨��P�����A��B�غϣ�������P��PM��OB����һ�����ڵ��������ڵ�M������M��MC��x���ڵ�C����AB�ڵ�N������P��PF��MC�ڵ�F����PF�ij�Ϊt��MN�ij�Ϊd����d��t֮��ĺ�����ϵʽ����Ҫ��д���Ա���t��ȡֵ��Χ����
��3���ڣ�2���������£���S��ACN=S��PMNʱ������ON����Q���߶�BP�ϣ�����Q��QR��MN��ON�ڵ�R������MQ��BR������MQR����BRN=45��ʱ�����R�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��▱ABCD�У�AB��AD��AE��BE��CM��DM�ֱ�Ϊ��DAB����ABC����BCD����CDA��ƽ���ߣ�AE��DM�ཻ�ڵ�F��BE��CM�ཻ�ڵ�H������EM����▱ABCD���ܳ�Ϊ42cm��FM=3cm��EF=4cm����EM=����cm��AB=����cm��
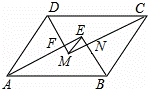
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com