练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，AB是半圆O的直径，C、D是半圆O上的两点，且OD∥BC，OD与AC交于点E．

    （1）若∠B=70°，求∠CAD的度数；

    （2）若AB=4，AC=3，求DE的长．


    解：（1）∵AB是半圆O的直径，

    ∴∠ACB=90°，

    又∵OD∥BC，

    ∴∠AEO=90°，即OE⊥AC，

    ∠CAB=90°﹣∠B=90°﹣70°=20°，∠AOD=∠B=70°．

    ∵OA=OD，

    ∴∠DAO=∠ADO===55°

    ∴∠CAD=∠DAO﹣∠CAB=55°﹣20°=35°；

    （2）在直角△ABC中，BC===．

    ∵OE⊥AC，

    ∴AE=EC，

    又∵OA=OB，

    ∴OE=BC=．

    又∵OD=AB=2，

    ∴DE=OD﹣OE=2﹣．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    在平面内正方形ABCD与正方形CEFH如图放置，连DE，BH，两线交于M．求证：

    （1）BH=DE．

    （2）BH⊥DE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，矩形ABCD为台球桌面，AD=260cm，AB=130cm，球目前在E点位置，AE=60cm．如果小丁瞄准BC边上的点F将球打过去，经过反弹后，球刚好弹到D点位置．

    （1）求证：△BEF∽△CDF；

    （2）求CF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，⊙O的半径是5，AB是⊙O的直径，弦CD⊥AB，垂足为P，若CD=8，则△ACD的面积是　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


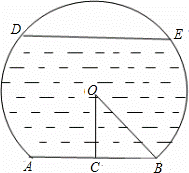
    一个弓形桥洞截面示意图如图所示，圆心为O，弦AB是水底线，OC⊥AB，AB=24m，sin∠COB=，DE是水位线，DE∥AB．

    （1）当水位线DE=4m时，求此时的水深；

    （2）若水位线以一定的速度下降，当水深8m时，求此时∠ACD的余切值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，A、B、C、D四个点均在⊙O上，∠AOD=70°，AO∥DC，则∠B的度数为（　　）

    A．  40°          B．45°          C．50°          D． 55°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC内接于⊙O，∠OAB=20°，则∠C的度数为　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在下列网格中，小正方形的边长均为1，点A、B、O都在格点上，则∠AOB的正弦值是（　　）

    A．          B．            C．            D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，一堤坝的坡角∠ABC=62°，坡面长度AB=25米（图为横截面），为了使堤坝更加牢固，一施工队欲改变堤坝的坡面，使得坡面的坡角∠ADB=50°，则此时应将坝底向外拓宽多少米？（结果保留到0.01米）

    （参考数据：sin62°≈0.88，cos62°≈0.47，tan50°≈1.20）

    查看答案和解析>>

    同步练习册答案